Question

已知f(x)＝x²＋x＋c，且f[f(x)]＝f(x²＋x＋1)

(1)设g(x)＝f[f(x)]，求g(x)的解析式；

(2)设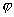(x)＝g(x)－λf(x)，试问：是否存在实数λ，使得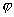(x)在(－∞，－1)上是减函数，并且在(－1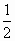，－)上是增函数．

Answer 1

答案：
解析：

解　　(1)因为f(x)＝x2＋x＋c，且f[f(x)]＝f(x2＋x＋1)，所以 　　(x2＋x＋c)2＋x2＋x＋c＋c＝(x2＋x＋1)2＋x2＋x＋1＋c， 　　(2c－2)x2＋(2c－2)x＋c2＋c－2＝0，故c＝1， 　　所以　　g(x)＝f[f(x)]＝x4＋2x3＋4x2＋3x＋3． 　　(2)假设存在实数λ，使得(x)在(－∞，－1)上是减函数，并且在(－1，－)上是增函数． 　　∵(x)＝g(x)－λf(x) 　　　　　＝x4＋2x3＋4x2＋3x＋3－λ(x2＋x＋1) 　　　　　＝x4＋2x3＋(4－λ)x2＋(3－λ)x＋(3－λ)， 　　∴(x)＝4x3＋6x2＋2(4－λ)x＋(3－λ)． 　　由(x)在(－∞，－1)上是减函数，并且在(－1，－)上是增函数可得(－1)＝0， 　　所以－4＋6－8＋2λ＋3－λ＝0，解得λ＝3． 　　∴(x)＝4x3＋6x3＋2x2＝2x(2x＋1)(x＋1)． 　　∴当x∈(－∞，－1)时，(x)＝4x3＋6x3＋2x2＝2x(2x＋1)(x＋1)＜0， 　　此时(x)在(－∞，－1)上是减函数； 　　当x∈(－1，－)时，(x)＝4x3＋6x3＋2x2＝2x(2x＋1)(x＋1)＞0， 　　此时(x)在(－1，－)上是增函数． 　　存在实数λ＝3，使得(x)在(－∞，－1)上是减函数，并且在(－1，－)上是增函数．