练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若直线与不等式组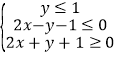表示的平面区域无公共点，则的取值范围是

    A. B. C. D. R

    【答案】C

    【解析】

    作出不等式组对应的平面区域，利用直线ax+by=1与平面区域无公共点建立条件关系，即可得到结论．

    不等式组表示的平面区域是由A（1，1），B（﹣1，1），C（0，﹣1）围成的三角形区域（包含边界）．

    ∵直线ax+by=1与表示的平面区域无公共点，

    ∴a，b满足：或．

    （a，b）在如图所示的三角形区域（除边界且除原点）．

    设z=2a+3b，平移直线z=2a+3b，当直线经过点A1（0，1）时，z最大为z=3，

    当经过点B1时，z最小，

    由解得，即B1（﹣2，﹣1），

    此时z=﹣4﹣3=﹣7，

    故2a+3b的取值范围是（﹣7，3）．

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，，

    （1）当时，求的最大值和最小值；

    （2）求实数的取值范围，使在区间上是单调函数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某城市为鼓励人们绿色出行，乘坐地铁，地铁公司决定按照乘客经过地铁站的数量实施分段优惠政策，不超过站的地铁票价如下表：

    乘坐站数

    票价（元）

    现有甲、乙两位乘客同时从起点乘坐同一辆地铁，已知他们乘坐地铁都不超过站，且他们各自在每个站下车的可能性是相同的.

    （1）若甲、乙两人共付费元，则甲、乙下车方案共有多少种？

    （2）若甲、乙两人共付费元，求甲比乙先到达目的地的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某城市的公交公司为了方便市民出行，科学规划车辆投放，在一个人员密集流动地段增设一个起点站，为了研究车辆发车间隔时间与乘客等候人数之间的关系，经过调查得到如下数据：

    间隔时间/分

    10

    11

    12

    13

    14

    15

    等候人数y/人

    23

    25

    26

    29

    28

    31

    调查小组先从这组数据中选取组数据求线性回归方程，再用剩下的组数据进行检验．检验方法如下：先用求得的线性回归方程计算间隔时间对应的等候人数，再求与实际等候人数的差，若差值的绝对值都不超过，则称所求方程是“恰当回归方程”．

    （1）从这组数据中随机选取2组数据，求选取的这组数据的间隔时间不相邻的概率；

    （2）若选取的是后面组数据，求关于的线性回归方程，并判断此方程是否是“恰当回归方程”；

    附：对于一组数据，，……，，其回归直线的斜率和截距的最小二乘估计分别为：，.

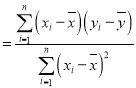    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某班共有学生40人，将一次数学考试成绩（单位：分）绘制成频率分布直方图，如图所示。

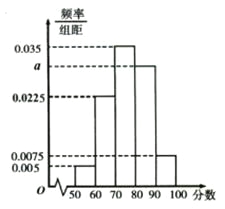
    (1)请根据图中所给数据，求出的值；

    (2)从成绩在[50，70）内的学生中随机选3名学生，求这3名学生的成绩都在[60，70）内的概率；

    (3)为了了解学生本次考试的失分情况，从成绩在[50，70）内的学生中随机选取3人的成绩进行分析，用X表示所选学生成绩在[ 60，70）内的人数，求X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二次函数y=f1(x)的图象以原点为顶点且过点(1,1),反比例函数y=f2(x)的图象与直线y=x的两个交点间距离为8,f(x)= f1(x)+ f2(x).

    (Ⅰ) 求函数f(x)的表达式；

    (Ⅱ) 证明:当a>3时,关于x的方程f(x)= f(a)有三个实数解.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）解不等式；

    （2）设函数的最小值为c，实数a，b满足，求证：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

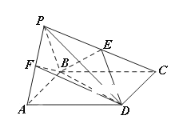
    【题目】如图,四棱锥 中,是正三角形,四边形ABCD是矩形,且平面平面.

    (1)若点E是PC的中点,求证:平面BDE;

    (2)若点F在线段PA上,且,当三棱锥的体积为时,求实数的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）求函数的值域；

    （2）若时，函数的最小值为，求的值和函数的最大值．

    查看答案和解析>>

    同步练习册答案