
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 ①利用线面垂直的性质可得:若m⊥α,m⊥n,则n∥α或n?α;
②利用平面平行的传递性和平行平面的性质可得:若α∥β,β∥γ,则α∥γ,又m⊥α,则m⊥γ;
③利用线面平行的性质可得:若m∥α,n∥α,则m∥n、相交或为异面直线;
④利用面面垂直的性质可得:若α⊥γ,β⊥γ,则α∥β或相交.
解答 解:①若m⊥α,m⊥n,则n∥α或n?α,因此①不正确;
②若α∥β,β∥γ,则α∥γ,又m⊥α,则m⊥γ,正确;
③若m∥α,n∥α,则m∥n、相交或为异面直线,因此不正确;
④若α⊥γ,β⊥γ,则α∥β或相交,因此不正确.
综上可知:只有②正确.
故选:B.
点评 本题综合考查了空间中线面的位置关系及其判定性质,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
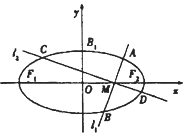 设椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点为F1,F2,点B1为其短轴的一个端点,满足$|{\overrightarrow{{B_1}{F_1}}+\overrightarrow{{B_1}{F_2}}}|=2|{\overrightarrow{{B_1}{F_1}}}|+|{\overrightarrow{{B_1}{F_2}}}|=2,\overrightarrow{{B_1}{F_1}}•\overrightarrow{{B_1}{F_2}}$=-2.
设椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的两个焦点为F1,F2,点B1为其短轴的一个端点,满足$|{\overrightarrow{{B_1}{F_1}}+\overrightarrow{{B_1}{F_2}}}|=2|{\overrightarrow{{B_1}{F_1}}}|+|{\overrightarrow{{B_1}{F_2}}}|=2,\overrightarrow{{B_1}{F_1}}•\overrightarrow{{B_1}{F_2}}$=-2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin2x | B. | y=2|cosx| | C. | $y=cos\frac{x}{2}$ | D. | y=tan(-x) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 17 | B. | -7 | C. | 7 | D. | -6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com