已知
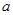
、
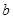
为正实数,函数
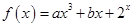
在
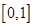
上的最大值为
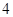
,则
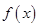
在
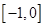
上的最小值为
.
试题分析:
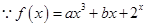
,所以
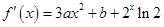
,
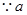
、
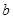
为正实数,
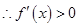
,
故函数
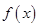
在区间
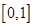
上单调递增,在区间
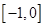
上亦单调递增,则有
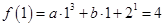
,所以
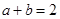
,故
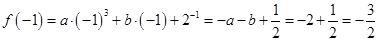
,即函数
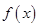
在
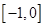
上的最小值为
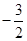
.
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知定义域为
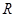
的函数
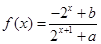
是奇函数.
(1)求
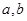
的值;
(2)判断函数
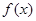
的单调性,并证明.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
设二次函数
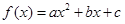
在区间
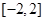
上的最大值、最小值分别是
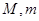
,集合
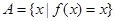
.
(Ⅰ)若
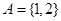
,且
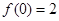
,求
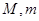
的值;
(Ⅱ)若
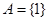
,且
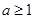
,记
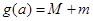
,求
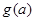
的最小值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知函数
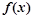
定义在R上的奇函数,当
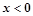
时,
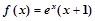
,给出下列命题:
①当
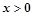
时,
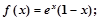
②函数
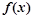
有2个零点
③
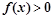
的解集为
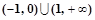
④
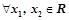
,都有
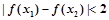
其中正确的命题是
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
奇函数
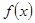
在
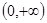
上为单调递减函数,且
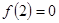
,则不等式
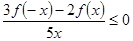
的解集为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知
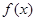
是偶函数,在区间
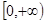
上是增函数,若
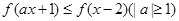
在
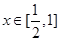
上恒成立,则实数
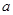
的取值范围为
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
已知函数
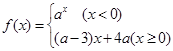
,满足对任意
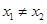
,都有
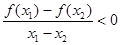
成立,则的取值范围是
.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知
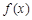
是定义在R上的奇函数,当
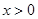
时,
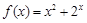
,若
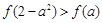
,则实数
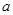
的取值范围是( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知函数
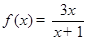
,求
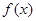
在区间[2,5]上的最大值和最小值
查看答案和解析>>

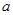 、
、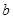 为正实数,函数
为正实数,函数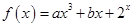 在
在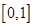 上的最大值为
上的最大值为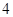 ,则
,则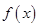 在
在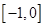 上的最小值为 .
上的最小值为 . 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案