
| 网络 | 月租费 | 本地话费 | 长途话费 |
| 甲:联通130 | 12元 | 0.36元/分 | 0.06元/秒 |
| 乙:移动“神州行” | 无 | 0.60元/分 | 0.07元/秒 |
| A. | 300秒 | B. | 400秒 | C. | 500秒 | D. | 600秒 |
分析 根据每月的通话时间和甲方式的收费标准,可知所需花费=月租费+本地话费+长途话费,可求所需话费y(元)与通话时间x(分钟)的函数关系式;将乙方式所需话费y(元)与通话时间x(分钟)的函数关系式求出,将两个式子进行比较,可得出较为省钱的入网方式.
解答 解:每月接打本地电话的时间是接打长途电话的5倍,王先生每月拨打长途电话时间为x(分钟),他所需话费y(元),联通130他所需话费y(元)与通话时间x(分钟)的函数关系式为y=12+0.36×5x+3.6x(x>0);
移动“神州行”他所需话费y(元)与通话时间x(分钟)的函数关系式为:y=0.6×5x+4.2x,
若要用联通130应最少打多长时间的长途电话才合算,可得:12+0.36×5x+3.6x<0.6×5x+4.2x,
解得:x>$\frac{20}{3}$(分钟)=400秒.
故选:B.
点评 本题主要是应用数学模型来解决实际问题,考查一次函数的应用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,10] | B. | $[{\sqrt{5},\sqrt{13}}]$ | C. | [1,5] | D. | $[{2,\sqrt{13}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,已知双曲线C的右焦点为F,过它的右顶点A作实轴的垂线,与其一条渐近线相交于点B;若双曲线C的焦距为4,△OFB为等边三角形(O为坐标原点,即双曲线C的中心),则双曲线C的方程为${x^2}-\frac{y^2}{3}=1$.
如图,已知双曲线C的右焦点为F,过它的右顶点A作实轴的垂线,与其一条渐近线相交于点B;若双曲线C的焦距为4,△OFB为等边三角形(O为坐标原点,即双曲线C的中心),则双曲线C的方程为${x^2}-\frac{y^2}{3}=1$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
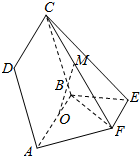 如图所示,点E,F在以AB为直径的圆O(O为圆心)上,AB∥EF,平面ABCD⊥平面ABEF,且AB=2,AD=EF=1
如图所示,点E,F在以AB为直径的圆O(O为圆心)上,AB∥EF,平面ABCD⊥平面ABEF,且AB=2,AD=EF=1查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)={x^2},g(x)=\sqrt{x^2}$ | B. | $f(x)=\frac{{{{(\sqrt{x})}^2}}}{x},g(x)=\frac{x}{{{{(\sqrt{x})}^2}}}$ | ||
| C. | f(x)=1,g(x)=(x-1)0 | D. | $f(x)=\frac{{{x^2}-9}}{x+3},g(x)=x-3$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com