考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(1)由于椭圆
C:+=1(a>b>0)过点
A(1,),离心率为
,可得
+=1,
=即
=,即可解出.
(2)对直线l的斜率分类讨论,与椭圆的方程联立可得根与系数的关系,再利用弦长公式、点到直线的距离公式、三角形的面积计算公式即可得出.
解答:
解:(1)∵椭圆
C:+=1(a>b>0)过点
A(1,),
∴
+=1①,
又∵离心率为
,
∴
=,∴
=②,
联立①②得a
2=4,b
2=3.
∴椭圆的方程为:
+=1(2)①当直线的倾斜角为
时,
A(-1,),B(-1,-),
S△ABF2=
|AB|×|F1F2|=
×3×2≠,不适合题意.
②当直线的倾斜角不为
时,设直线方程l:y=k(x+1),
代入
+=1得:(4k
2+3)x
2+8k
2x+4k
2-12=0
设A(x
1,y
1),B(x
2,y
2),则
x1+x2=,
x1x2=,
∴|AB|=
=
=
.
点F
2到直线l的距离d=
,
∴
S△ABF2=
|AB|•d=
=
,
化为17k
4+k
2-18=0,解得k
2=1,∴k=±1,
∴直线方程为:x-y+1=0或x+y+1=0.
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、弦长公式、点到直线的距离公式、三角形的面积计算公式,考查了分类讨论的思想方法,考查了推理能力与计算能力,属于难题.



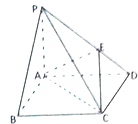 已知四棱锥P-ABCD中,PA=AB,PA⊥底面ABCD,ABCD是平行四边形,且∠BAC=90°.
已知四棱锥P-ABCD中,PA=AB,PA⊥底面ABCD,ABCD是平行四边形,且∠BAC=90°.