
分析 (1)利用绝对值不等式的解法,解|x-m|<$\frac{1}{2}$,可得定义域,并画出图象.
(2)分别求出f(a1),f(a2),f(a3),…,f(an),考查数列{f(an )} 的性质,再求和.
解答 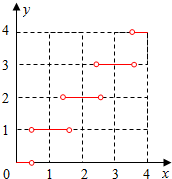 解:(1)函数f(x)的定义域是D={x||x-m|<$\frac{1}{2}$}
解:(1)函数f(x)的定义域是D={x||x-m|<$\frac{1}{2}$}
={x|m-$\frac{1}{2}$<x<m+$\frac{1}{2}$,m∈Z}
图象如图所示,
(2)由于an=2+10•($\frac{2}{5}$)n,
所以f(an)=$\left\{\begin{array}{l}{6,n=1}\\{4,n=2}\\{3,n=3}\\{2,n≥4}\end{array}\right.$,
当n=1时,S1=6,
n=2时,S2=f(a1)+f(a2)=6+4=10,
n=3时,S3=f(a1)+f(a2)+f(a3)=6+4+3=13,
n>3时,Sn=6+4+3+2(n-3)=2n+7,
因此Sn=$\left\{\begin{array}{l}{6,n=1}\\{10,n=2}\\{2n+7,n≥3}\end{array}\right.$.
点评 本题考查阅读理解、计算、分类讨论思想和能力.正确理解新定义,将问题转化成已有的知识,用已有的方法解决此类问题共同的策略.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
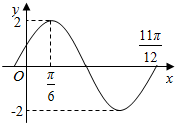 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,若方程f(x)=m在区间[0,π]上有两个不同的数解x1、x2,则x1+x2的值为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,若方程f(x)=m在区间[0,π]上有两个不同的数解x1、x2,则x1+x2的值为( )| A. | $\frac{π}{3}$ | B. | $\frac{2}{3}π$ | C. | $\frac{4}{3}π$ | D. | $\frac{π}{3}$或$\frac{4}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{6}$ | D. | 2$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2+c2=2b2 | B. | ac=b2 | C. | a+c=2b | D. | ac=2b2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com