
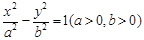 的渐近线,△P1OP2的面积为
的渐近线,△P1OP2的面积为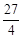 ,在双曲线E上存在点P为线段P1P2的一个三等分点,且双曲线E的离心率为
,在双曲线E上存在点P为线段P1P2的一个三等分点,且双曲线E的离心率为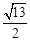 .
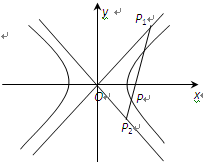
.
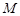 ,两焦点
,两焦点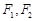 ,若
,若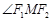 为钝角,求
为钝角,求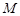 点横坐标
点横坐标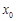 的取值范围.
的取值范围.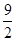 ;(2)
;(2)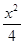 -
-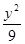 =1;(3)-
=1;(3)-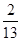
 ,-2)∪(2,
,-2)∪(2,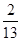
 )
)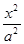 -
-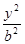 =1,由已知得
=1,由已知得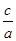 =
=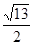
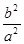 =
=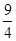 ∴渐近线方程为y=±
∴渐近线方程为y=±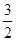 x …………2分
x …………2分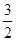 x1) P2(x2,-
x1) P2(x2,-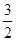 x2)
x2)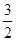 x的倾斜角为θ,则tanθ=
x的倾斜角为θ,则tanθ=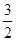 ∴sin2θ=
∴sin2θ=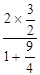 =
=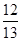
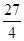 =
=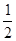 |OP1||OP2|sin2θ=
|OP1||OP2|sin2θ=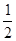
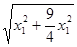
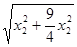 ·
·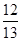
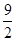 …………5分
…………5分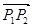 所成的比为λ=2,P(x,y), 则
所成的比为λ=2,P(x,y), 则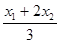 y=
y=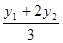 =
=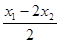
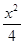 -
-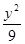 =1 即为双曲线E的方程 …………9分
=1 即为双曲线E的方程 …………9分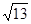 ,∴F1(-
,∴F1(-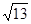 ,0) F2(
,0) F2(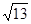 ,0) 设M(x0,y0)
,0) 设M(x0,y0)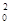 =
=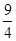 x
x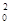 -9,
-9,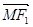 =(-
=(-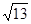 -x0,-y0)
-x0,-y0) 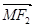 =(
=(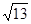 -x0,-y0)
-x0,-y0)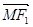 ·
·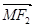 =x
=x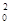 -13+y
-13+y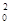 =
=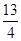 x
x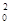 -22 …………12分
-22 …………12分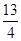 x
x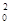 -22<0
-22<0 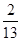
 又|x0|>2
又|x0|>2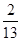
 ,-2)∪(2,
,-2)∪(2,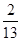
 ) ……14分
) ……14分

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
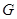 :
: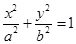
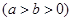 的两个焦点为
的两个焦点为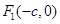 、
、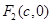 和顶点
和顶点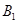 、
、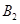 构成面积为32的正方形.
构成面积为32的正方形.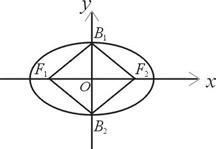
 的方程;
的方程; 的直线
的直线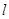 与椭圆
与椭圆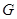 相交于不同的两点
相交于不同的两点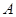 、
、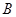 、
、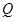 为
为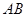 的中点,且
的中点,且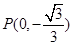 . 问:
. 问: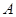 、
、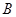 两点能否关于直线
两点能否关于直线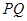 对称. 若能,求出
对称. 若能,求出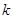 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 。
。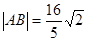 ,求直线l的方程。
,求直线l的方程。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
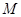 到
到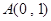 的距离比它到
的距离比它到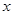 轴的距离多一个单位.
轴的距离多一个单位.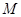 的轨迹
的轨迹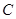 的方程;
的方程; 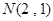 作曲线
作曲线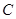 的切线
的切线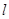 ,求切线
,求切线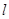 的方程,并求出
的方程,并求出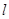 与曲线
与曲线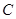 及
及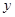 轴所围成图形的面积
轴所围成图形的面积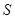 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com