
【题目】如图所示,在等腰梯形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,直角梯形
,直角梯形![]() 所在的平面垂直于平面
所在的平面垂直于平面![]() ,且
,且![]() ,
,![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上,试确定点
上,试确定点![]() 的位置,使平面
的位置,使平面![]() 与平面
与平面![]() 所成的二面角的余弦值为
所成的二面角的余弦值为![]() .
.
【答案】(1)证明见解析;(2)点![]() 为线段
为线段![]() 中点
中点
【解析】
(1)推导出![]() 平面
平面![]() ,
,![]() ,
,![]() ,从而
,从而![]() 平面
平面![]() ,由此能证明平面
,由此能证明平面![]() 平面
平面![]() ;
;
(2)以![]() 为坐标原点,以
为坐标原点,以![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴建立空间直角坐标系,利用向量法能求出点
轴建立空间直角坐标系,利用向量法能求出点![]() 为线段
为线段![]() 中点时,平面
中点时,平面![]() 与平面
与平面![]() 所成的二面角的余弦值.
所成的二面角的余弦值.
解:(1)因为平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,
![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ,
,
在△![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
由余弦定理得,![]() ,
,
所以![]() ,所以
,所以![]() .
.
又![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ;
;
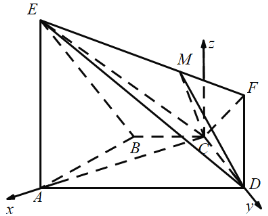
(2)以![]() 为坐标原点,以
为坐标原点,以![]() ,
,![]() 所在直线分别为
所在直线分别为![]() 轴、
轴、![]() 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,![]() ,
,![]() ,
,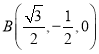 ,
,![]() ,
,![]() ,
,![]() ,
,
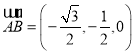 ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设![]() ,则
,则![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则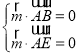 ,即
,即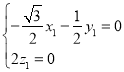 ,取
,取![]() ,得
,得![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
由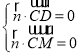 ,得
,得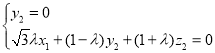 ,
,
令![]() ,得
,得![]() ,
,
因为平面![]() 与平面
与平面![]() 所成的二面角的余弦值为
所成的二面角的余弦值为![]() ,
,
所以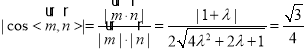 ,
,
整理得![]() ,
,
解得![]() 或
或![]() (舍去),
(舍去),
所以点![]() 为线段
为线段![]() 中点时,平面
中点时,平面![]() 与平面
与平面![]() 所成的二面角的余弦值为
所成的二面角的余弦值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,△ABC中,AB⊥BC,∠ACB=60°,D为AC中点,△ABD沿BD翻折过程中,直线AB与直线BC所成的最大角、最小角分别记为α1,β1,直线AD与直线BC所成最大角、最小角分别记为α2,β2,则有( )
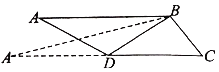
A.α1<α2,β1≤β2B.α1<α2,β1>β2
C.α1≥α2,β1≤β2D.α1≥α2,β1>β2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设F是椭圆![]() 的左焦点,过点F且斜率为正的直线与E相交于A、B两点,过点A、B分别作直线AM和BN满足AM⊥l,BN⊥l,且直线AM、BN分别与x轴相交于M和N.试求|MN|的最小值.
的左焦点,过点F且斜率为正的直线与E相交于A、B两点,过点A、B分别作直线AM和BN满足AM⊥l,BN⊥l,且直线AM、BN分别与x轴相交于M和N.试求|MN|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述中错误的是( )
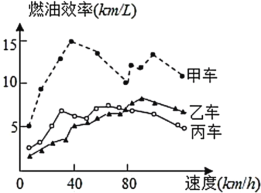
A.消耗1升汽油乙车最多可行驶5千米.
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多.
C.甲车以80千米/小时的速度行驶1小时,消耗10升汽油.
D.某城市机动车最高限速80千米/小时,相同条件下,在该市用丙车比用乙车更省油.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,对于函数
,对于函数![]() 有下述四个结论:①函数
有下述四个结论:①函数![]() 在其定义域上为增函数;②对于任意的
在其定义域上为增函数;②对于任意的![]() ,
,![]() ,都有
,都有![]() 成立;③
成立;③![]() 有且仅有两个零点;④若
有且仅有两个零点;④若![]() ,则
,则![]() 在点
在点![]() 处的切线与
处的切线与![]() 在点
在点![]() 处的切线为同一直线.其中所有正确的结论有( )
处的切线为同一直线.其中所有正确的结论有( )
A.①②③B.①③C.②③④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱台![]() 的下底面
的下底面![]() 是边长为2的正三角形,上地面
是边长为2的正三角形,上地面![]() 是边长为1的正三角形.
是边长为1的正三角形.![]() 在下底面的射影为
在下底面的射影为![]() 的重心,且
的重心,且![]() .
.
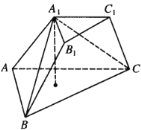
(1)证明:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,曲线
为参数),以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,设曲线
,设曲线![]() 与曲线
与曲线![]() 的公共弦所在直线为l.
的公共弦所在直线为l.
(1)在直角坐标系下,求曲线![]() 与曲线
与曲线![]() 的普通方程;
的普通方程;
(2)若以坐标原点为中心,直线l顺时针方向旋转![]() 后与曲线
后与曲线![]() 、曲线
、曲线![]() 分别在第一象限交于A、B两点,求
分别在第一象限交于A、B两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1(﹣c,0),F2(c,0)分別为双曲线![]() 1(a>0,b>0)的左、右焦点,以坐标原点O为圆心,c为半径的圆与双曲线在第二象限交于点P,若tan∠PF1F2
1(a>0,b>0)的左、右焦点,以坐标原点O为圆心,c为半径的圆与双曲线在第二象限交于点P,若tan∠PF1F2![]() ,则该双曲线的离心率为_____.
,则该双曲线的离心率为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com