
【题目】某地某所高中2019年的高考考生人数是2016年高考考生人数的1.2倍,为了更好地对比该校考生的升学情况,统计了该校2016年和2019年的高考升学情况,得到如图所示:则下列结论正确的( )
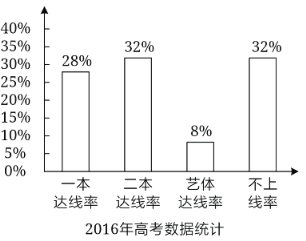
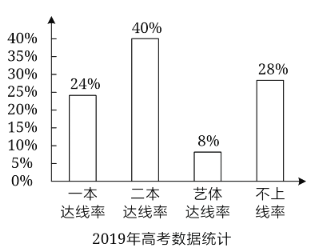
A.与2016年相比,2019年一本达线人数有所减少
B.与2016年相比,2019年二本达线人数增加了1倍
C.与2016年相比,2019年艺体达线人数相同
D.与2016年相比,2019年不上线的人数有所增加
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:高中数学 来源: 题型:
【题目】(题文)(2017·长春市二模)如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() 平面
平面![]() ,
,![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() 和
和![]() 中点.
中点.

(1)求证:直线![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2xlnx﹣x![]() 2.
2.
(1)求曲线y=f(x)在点(1,f(1))处的切线方程
(2)若方程f′(x)=a在[![]() ,+∞)有且仅有两个实根(其中f′(x)为f(x)的导函数,e为自然对数的底),求实数a的取值范围.
,+∞)有且仅有两个实根(其中f′(x)为f(x)的导函数,e为自然对数的底),求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() (其中a是常数).
(其中a是常数).
(1)求过点![]() 与曲线
与曲线![]() 相切的直线方程;
相切的直线方程;
(2)是否存在![]() 的实数,使得只有唯一的正数a,当
的实数,使得只有唯一的正数a,当![]() 时不等式
时不等式![]() 恒成立,若这样的实数k存在,试求k,a的值;若不存在.请说明理由.
恒成立,若这样的实数k存在,试求k,a的值;若不存在.请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的方程为
的方程为![]() .
.
(1)以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,求曲线
轴的正半轴为极轴建立极坐标系,求曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的极坐标方程;
的极坐标方程;
(2)在(1)的条件下,直线![]() 的极坐标方程为
的极坐标方程为![]() ,设曲线
,设曲线![]() 与直线
与直线![]() 的交于点
的交于点![]() 和点
和点![]() ,曲线
,曲线![]() 与直线
与直线![]() 的交于点
的交于点![]() 和点
和点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com