
【题目】已知直三棱柱![]() 中的底面为等腰直角三角形,
中的底面为等腰直角三角形,![]() ,点
,点![]() 分别是边
分别是边![]() ,
,![]() 上动点,若直线
上动点,若直线![]() 平面
平面![]() ,点
,点![]() 为线段
为线段![]() 的中点,则
的中点,则![]() 点的轨迹为
点的轨迹为![]()
![]()
A. 双曲线的一支![]() 一部分
一部分![]() B. 圆弧
B. 圆弧![]() 一部分
一部分![]()
C. 线段![]() 去掉一个端点
去掉一个端点![]() D. 抛物线的一部分
D. 抛物线的一部分
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的最大值为
的最大值为![]() ,其图像相邻的两条对称轴之间的距离为
,其图像相邻的两条对称轴之间的距离为![]() ,且
,且![]() 的图像关于点
的图像关于点![]() 对称,则下列结论正确的是( ).
对称,则下列结论正确的是( ).
A.函数![]() 的图像关于直线
的图像关于直线![]() 对称
对称
B.当![]() 时,函数
时,函数![]() 的最小值为
的最小值为![]()
C.若![]() ,则
,则![]() 的值为
的值为![]()
D.要得到函数![]() 的图像,只需要将
的图像,只需要将![]() 的图像向右平移
的图像向右平移![]() 个单位
个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年茂名市举办“好心杯”少年美术书法作品比赛,某赛区收到200件参赛作品,为了解作品质量,现从这些作品中随机抽取12件作品进行试评.成绩如下:67,82,78,86,96,81,73,84,76,59,85,93.
(1)求该样本的中位数和方差;
(2)若把成绩不低于85分(含85分)的作品认为为优秀作品,现在从这12件作品中任意抽取3件,求抽到优秀作品的件数的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对某校学生做了一个是否同意生“二孩”抽样调查,该调查机构从该校随机抽查了100名不同性别的学生,调查统计他们是同意父母生“二孩”还是反对父母生“二孩”,现已得知100人中同意父母生“二孩”占60%,统计情况如下表:
同意 | 不同意 | 合计 | |
男生 | a | 5 | |
女生 | 40 | d | |
合计 | 100 |
(1)求 a,d 的值,根据以上数据,能否有97.5%的把握认为是否同意父母生“二孩”与性别有关?请说明理由;
(2)将上述调查所得的频率视为概率,现在从所有学生中,采用随机抽样的方法抽取4 位学生进行长期跟踪调查,记被抽取的4位学生中持“同意”态度的人数为 X,求 X 的分布列及数学期望.
附: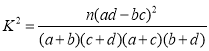
| 0.15 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
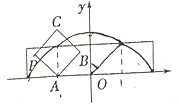
【题目】如图放置的边长为1的正方形![]() 沿
沿![]() 轴滚动,点
轴滚动,点![]() 恰好经过原点.设顶点
恰好经过原点.设顶点![]() 的轨迹方程是
的轨迹方程是![]() ,则对函数
,则对函数![]() 有下列判断:①函数
有下列判断:①函数![]() 是偶函数;②对任意的
是偶函数;②对任意的![]() ,都有
,都有![]() ;③函数
;③函数![]() 在区间
在区间![]() 上单调递减;④函数
上单调递减;④函数![]() 的值域是
的值域是![]() ;⑤
;⑤![]() .其中判断正确的序号是__________.
.其中判断正确的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2016年8月巴西里约热内卢举办的第31届奥运会上,乒乓球比赛团体决赛实行五场三胜制,且任何一方获胜三场比赛即结束.甲、乙两个代表队最终进入决赛,根据双方排定的出场顺序及以往战绩统计分析,甲队依次派出的五位选手分别战胜对手的概率如下表:
出场顺序 | 1号 | 2号 | 3号 | 4号 | 5号 |
获胜概率 |
|
|
|
|
|
若甲队横扫对手获胜(即3∶0获胜)的概率是![]() ,比赛至少打满4场的概率为
,比赛至少打满4场的概率为![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)求甲队获胜场数的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构用“10分制”调查了各阶层人士对某次国际马拉松赛事的满意度,现从调查人群中随机抽取16名,如图茎叶图记录了他们的满意度分数![]() 以小数点前的一位数字为茎,小数点后的一位数字为叶
以小数点前的一位数字为茎,小数点后的一位数字为叶![]() :
:

(1)指出这组数据的众数和中位数;
(2)若满意度不低于![]() 分,则称该被调查者的满意度为“极满意”,求从这16人中随机选取3人,至少有2人满意度是“极满意”的概率;
分,则称该被调查者的满意度为“极满意”,求从这16人中随机选取3人,至少有2人满意度是“极满意”的概率;
(3)以这16人的样本数据来估计整个被调查群体的总体数据,若从该被调查群体![]() 人数很多
人数很多![]() 任选3人,记
任选3人,记![]() 表示抽到“极满意”的人数,求
表示抽到“极满意”的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com