练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知全集U=R，A={x|x≥3}，B={x|x2﹣8x+7≤0}，C={x|x≥a﹣1}
    （1）求A∩B，A∪B；
    （2）若A∩C=C，求实数a的取值范围．

    【答案】
    （1）解：由题意可得B={x|x2﹣8x+7≤0}={x|1≤x≤7}，，

    ∴A∩B={x|3≤x≤7}，A∪B={x|x≥1}


    （2）解：∵A∩C=C，∴CA

    ∴a﹣1≥3，∴a≥4


    【解析】（1）解关于集合B的不等式，求出x的范围，从而求出A∩B，A∪B；（2）由A∩C=C，得到CA，从而求出a的范围即可．
    【考点精析】关于本题考查的集合的并集运算和集合的交集运算，需要了解并集的性质：（1）AA∪B，BA∪B，A∪A=A，A∪=A,A∪B=B∪A;（2）若A∪B=B，则AB，反之也成立；交集的性质：（1）A∩BA，A∩BB，A∩A=A，A∩=,A∩B=B∩A;（2）若A∩B=A，则AB，反之也成立才能得出正确答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，平行四边形中， ， ， ， ， 分别为， 的中点，

    平面.

    （1）求证： 平面；

    （2）求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设点是轴上的一个定点，其横坐标为（），已知当时，动圆过点且与直线相切，记动圆的圆心的轨迹为．

    （Ⅰ）求曲线的方程；

    （Ⅱ）当时，若直线与曲线相切于点（），且与以定点为圆心的动圆也相切，当动圆的面积最小时，证明： 、两点的横坐标之差为定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f（x）=ax5﹣bx+1，若f（lg（log510））=5，求f（lg（lg5））的值（ ）
    A.﹣3
    B.5
    C.﹣5
    D.﹣9

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数对任意实数恒有，且当时， ，又.

    (1)判断的奇偶性；

    (2)求证： 是R上的减函数；

    (3)求在区间[－3,3]上的值域；

    (4)若x∈R，不等式恒成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（为常数，是自然对数的底数），曲线在点处的切线与轴平行.

    （1）求的值；

    （2）求的单调区间；

    （3）设,其中为的导函数.证明：对任意.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列四个命题：
    （1）函数f（x）在x＞0时是增函数，x＜0时也是增函数，所以f（x）是增函数；
    （2）若m=loga2，n=logb2且m＞n，则a＜b；
    （3）函数f（x）=x2+2（a﹣1）x+2在区间（﹣∞，4]上是减函数，则实数a的取值范围是a≤﹣3；
    （4）y=log （x2+x﹣2）的减区间为（1，+∞）．
    其中正确的个数是（ ）
    A.0
    B.1
    C.2
    D.3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在半径为3m的 圆形（O为圆心）铝皮上截取一块矩形材料OABC，其中点B在圆弧上，点A、C在两半径上，现将此矩形铝皮OABC卷成一个以AB为母线的圆柱形罐子的侧面（不计剪裁和拼接损耗），设矩形的边长AB=xm，圆柱的体积为Vm3 ．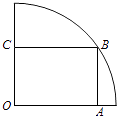
    （1）写出体积V关于x的函数关系式，并指出定义域；
    （2）当x为何值时，才能使做出的圆柱形罐子体积V最大？最大体积是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义域为R的函数f（x）= 是奇函数，
    （1）求实数a的值；
    （2）若对任意的t∈R，不等式f（t2﹣2t）+f（2t2﹣k）＜0恒成立，求实数k的取值范围；
    （3）设关于x的方程f（4x﹣b）+f（﹣2x+1）=0有实数根，求实数b的取值范围．

    查看答案和解析>>

    同步练习册答案