
【题目】已知双曲线![]() 过点
过点![]() 且渐近线为
且渐近线为![]() ,则下列结论正确的个数为( )
,则下列结论正确的个数为( )
①![]() 的实轴长为
的实轴长为![]() ;②
;②![]() 的离心率为
的离心率为![]() ;
;
③曲线![]() 经过
经过![]() 的一个焦点;④直线
的一个焦点;④直线![]() 与
与![]() 有两个公共点.
有两个公共点.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】将参加数学竞赛的500名同学编号为001,002,…,500,采用系统抽样的方法抽取一个容量为50的样本,且随机抽到的号码为005,这500名学生分别在三个考点考试,从001到200在第一考点,从201到365在第二考点,从366到500在第三考点,则第二考点被抽中的人数为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】地球海洋面积远远大于陆地面积,随着社会的发展,科技的进步,人类发现海洋不仅拥有巨大的经济利益,还拥有着深远的政治利益.联合国于第63届联合国大会上将每年的6月8日确定为“世界海洋日”.2019年6月8日,某大学的行政主管部门从该大学随机抽取100名大学生进行一次海洋知识测试,并按测试成绩(单位:分)分组如下:第一组[65,70),第二组[70,75),第二组[75,80),第四组[80,85),第五组[85,90],得到频率分布直方图如下图:
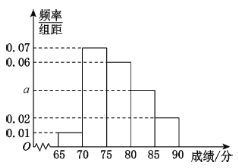
(1)求实数![]() 的值;
的值;
(2)若从第四组、第五组的学生中按组用分层抽样的方法抽取6名学生组成中国海洋实地考察小队,出发前,用简单随机抽样方法从6人中抽取2人作为正、副队长,列举出所有的基本事件并求“抽取的2人为不同组”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.
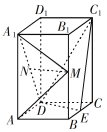
(1)证明:MN∥平面C1DE;
(2)求二面角A-MA1-N的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
11分制乒乓球比赛,每赢一球得1分,当某局打成10:10平后,每球交换发球权,先多得2分的一方获胜,该局比赛结束.甲、乙两位同学进行单打比赛,假设甲发球时甲得分的概率为0.5,乙发球时甲得分的概率为0.4,各球的结果相互独立.在某局双方10:10平后,甲先发球,两人又打了X个球该局比赛结束.
(1)求P(X=2);
(2)求事件“X=4且甲获胜”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com