
| x2 |
| 9 |
| y2 |
| 4 |
| 4x1 |
| 9y1 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| b2x1 |
| a2y1 |
| 1 |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| b2x1 |
| a2y1 |
| b2x1 |
| a2y1 |
| ab2+b2x1 |
| ay1 |
| ab2-b2x1 |
| ay1 |
| ab2+b2x1 |
| ay1 |
| ab2-b2x1 |
| ay1 |
| a2b2-b2x12 |
| a2y12 |
| 1 |
| 2 |
| 1 |
| 2 |
| |AM||A°‰M°‰| |


 –«º∂ø⁄À„ÃÏÃÏ¡∑œµ¡–¥∞∏
–«º∂ø⁄À„ÃÏÃÏ¡∑œµ¡–¥∞∏ √¢π˚ΩÃ∏®¥Ô±Í≤‚ ‘æÌœµ¡–¥∞∏
√¢π˚ΩÃ∏®¥Ô±Í≤‚ ‘æÌœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
|
|
|
|
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
| 1 |
| b |
| 1 |
| a |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
| y |
| 2 |
| y |
| 2 |
A°¢y2=
| ||
| B°¢y2=ax | ||
| C°¢y2=2ax | ||
| D°¢y2=4ax |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
| 1 |
| 3 |
| 1+x |
| 1-x |
A°¢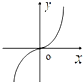 |
B°¢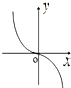 |
C°¢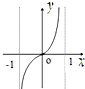 |
D°¢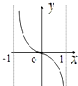 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
| 7 |
| 9 |
| 10 |
| 27 |
| 2 |
| 3 |
| 37 |
| 48 |
| 8 |
| 5 |
| 6 |
| 5 |
| 1 |
| 2 |
| 5 | a4 |
| 5 | b3 |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com