
【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,证明:
时,证明: ![]() 在定义域上为减函数;
在定义域上为减函数;
(Ⅱ)若![]() .讨论函数
.讨论函数![]() 的零点情况.
的零点情况.
【答案】(1)见解析(2)当![]() 时,函数
时,函数![]() 无零点;当
无零点;当![]() 或
或![]() 时,函数
时,函数![]() 有一个零点;当
有一个零点;当![]() 时,函数
时,函数![]() 有两个零点.
有两个零点.
【解析】试题分析:(Ⅰ)当![]() 时,对函数求导,利用导数与函数单调性的关系,可证明函数在定义域上为减函数;(Ⅱ)
时,对函数求导,利用导数与函数单调性的关系,可证明函数在定义域上为减函数;(Ⅱ) ![]() 的根情况,方程化简为
的根情况,方程化简为![]() ,构造函数
,构造函数![]() ,利用导数判断这个函数的取值情况,与
,利用导数判断这个函数的取值情况,与![]() 结合可得,函数
结合可得,函数![]() 的零点情况.
的零点情况.
试题解析:(Ⅰ)由题意可知函数![]() 的定义域为
的定义域为![]() .
.
![]() ,令
,令![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,所以
,所以![]() ,
,
即![]() ,所以
,所以![]() ,所以
,所以![]() 在定义域上为减函数.
在定义域上为减函数.
(Ⅱ)![]() 的零点情况,即方程
的零点情况,即方程![]() 的根情况,
的根情况,
因为![]() ,所以方程可化为
,所以方程可化为![]() ,
,
令![]() ,则
,则![]() ,令
,令![]() ,可得
,可得![]() ,
,
当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,所以
,所以![]() ,
,
且当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
所以![]() 的图像大致如图所示,
的图像大致如图所示,

结合图像可知,当![]() 时,方程
时,方程![]() 没有根;
没有根;
当![]() 或
或![]() 时,方程
时,方程![]() 有一个根;
有一个根;
当![]() 时,方程
时,方程![]() 有两个根.
有两个根.
所以当![]() 时,函数
时,函数![]() 无零点;当
无零点;当![]() 或
或![]() 时,函数
时,函数![]() 有一个零点;当
有一个零点;当![]() 时,函数
时,函数![]() 有两个零点.
有两个零点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在多面体ABCDEF中,底面ABCD是梯形,四边形ADEF是正方形,AB∥DC,AB=AD=1,CD=2,AC=EC=![]() 。
。
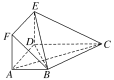
(1)求证:平面EBC⊥平面EBD;
(2)设M为线段EC上一点,且3EM=EC,试问在线段BC上是否存在一点T,使得MT∥平面BDE,若存在,试指出点T的位置;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com