
(本小题满分13分)已知函数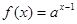 的图象经过点(2,
的图象经过点(2,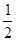 ),其中
),其中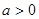 且
且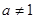 。
。
(1)求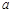 的值;
的值;
(2)若函数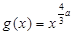 ,解关于
,解关于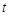 的不等式
的不等式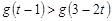 。
。
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
(本题满分12分) 商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购买人数越少。把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元。现在这种羊毛衫的成本价是100元/ 件,商场以高于成本价的相同价格(标价)出售. 问:
(Ⅰ)商场要获取最大利润,羊毛衫的标价应定为每件多少元?
(Ⅱ)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
某商店如果将进价为8元的商品按每件10元售出,每天可销售200件,现在提高售价以赚取更多利润.已知每涨价0.5元,该商店的销售量会减少10件,问将售价定为多少时,才能使每天的利润最大?其最大利润为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com