
分析 分别画出两函数的图象,根据图象的性质和基本不等式解题.
解答 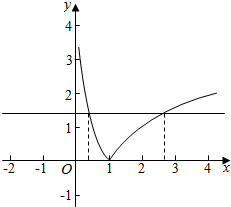 解:画出f(x)的图象,该函数先减后增,在x=1处取得最小值0,
解:画出f(x)的图象,该函数先减后增,在x=1处取得最小值0,
再画出直线y=m,两图象交于A,B,如右图(A在B左边),
此时,A(x1,y1),B(x2,y2),由图可知,0<x1<1<x2,
因为y1=y2,所以,-log2x1=log2x2,
解得x1x2=1,所以x1+x2≥2,
根据基本不等式:${2}^{{x}_{1}}+{2}^{{x}_{2}}$≥2$\sqrt{{2}^{{x}_{1}+{x}_{2}}}$≥2$\sqrt{{2}^{2}}$=4,
且x1≠x2,所以,${2}^{{x}_{1}}+{2}^{{x}_{2}}$>4,
综合以上分析:
①正确;②正确;③错误,④正确;
故填:①②④
点评 本题主要考查了对数函数的图象和性质,以及基本不等式的应用,属于中档题.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com