
【题目】如图所示,四棱锥![]() 的底面是边长为2的正方形,
的底面是边长为2的正方形,![]() 底面
底面![]() ,
,![]() 为
为![]() 的中点.
的中点.
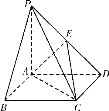
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)若三棱锥![]() 的体积为
的体积为![]() ,求四棱锥
,求四棱锥![]() 的侧面积.
的侧面积.
科目:高中数学 来源: 题型:
【题目】记![]() 分别为函数
分别为函数![]() 的导函数.若存在
的导函数.若存在![]() ,满足
,满足![]() 且
且![]() ,则称
,则称![]() 为函数
为函数![]() 与
与![]() 的一个“S点”.
的一个“S点”.
(1)证明:函数![]() 与
与![]() 不存在“S点”;
不存在“S点”;
(2)若函数![]() 与
与![]() 存在“S点”,求实数a的值;
存在“S点”,求实数a的值;
(3)已知函数![]() ,
,![]() .对任意
.对任意![]() ,判断是否存在
,判断是否存在![]() ,使函数
,使函数![]() 与
与![]() 在区间
在区间![]() 内存在“S点”,并说明理由.
内存在“S点”,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 的内角
的内角![]() 的对边分别为
的对边分别为![]() ,下列四个命题中正确的是( )
,下列四个命题中正确的是( )
A.若![]() ,则
,则![]() 一定是锐角三角形
一定是锐角三角形
B.若![]() ,则
,则![]() 一定是等边三角形
一定是等边三角形
C.若![]() ,则
,则![]() 一定是等腰三角形
一定是等腰三角形
D.若![]() ,则
,则![]() 一定是等腰三角形
一定是等腰三角形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y=f(x)是定义在(-∞,+∞)上的奇函数,且在[0,+∞)上为增函数,
(1)求证:函数在(-∞,0)上也是增函数;
(2)如果f(![]() )=1,解不等式-1<f(2x+1)≤0.
)=1,解不等式-1<f(2x+1)≤0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小李在做一份调查问卷,共有4道题,其中有两种题型,一种是选择题,共2道,另一种是填空题,共2道.
(1)小李从中任选2道题解答,每一次选1题(不放回),求所选的题不是同一种题型的概率;
(2)小李从中任选2道题解答,每一次选1题(有放回),求所选的题不是同一种题型的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
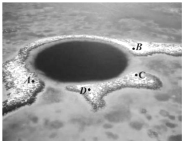
【题目】海洋蓝洞是地球罕见的自然地理现象,被喻为“地球留给人类保留宇宙秘密的最后遗产”,我国拥有世界上最深的海洋蓝洞,若要测量如图所示的蓝洞的口径![]() ,
,![]() 两点间的距离,现在珊瑚群岛上取两点
两点间的距离,现在珊瑚群岛上取两点![]() ,
,![]() ,测得
,测得![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() 两点的距离为___.
两点的距离为___.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在党中央的正确指导下,通过全国人民的齐心协力,特别是全体一线医护人员的奋力救治,二月份“新冠肺炎”疫情得到了控制.下图是国家卫健委给出的全国疫情通报,甲、乙两个省份从2月7日到2月13日一周的新增“新冠肺炎”确诊人数的折线图如下:
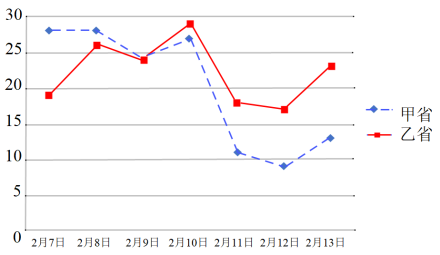
根据图中甲、乙两省的数字特征进行比对,通过比较把你得到最重要的两个结论写在答案纸指定的空白处.
①_________________________________________________.
②_________________________________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com