
【题目】已知函数![]() .
.
(1)若![]() ,求证:当
,求证:当![]() 时,
时,![]() ;
;
(2)若函数![]() 与函数
与函数![]() 有两个不同交点
有两个不同交点![]() 其中
其中![]() ,证明:存在
,证明:存在![]() ,使得
,使得![]() 在
在![]() 处的切线斜率与
处的切线斜率与![]() 在
在![]() 处的切线斜率相等.
处的切线斜率相等.
【答案】(1)见解析(2)见解析
【解析】
(1)根据![]() ,得
,得![]() ,
,![]() ,用导数法研究其单调性,得
,用导数法研究其单调性,得![]() 即可.
即可.
(2)根据函数![]() 与函数
与函数![]() 有两个不同交点
有两个不同交点![]() ,转化为
,转化为![]() 在
在![]() 上有两个不同的根
上有两个不同的根![]() ,
,![]() ,再假设存在
,再假设存在![]() ,使得
,使得![]() 在
在![]() 处的切线斜率与
处的切线斜率与![]() 在
在![]() 处的切线斜率相等.转化为
处的切线斜率相等.转化为![]() 有解.令
有解.令![]() ,因为
,因为![]() ,所以
,所以![]() 有两个零点,一正一负,设正根为m,有
有两个零点,一正一负,设正根为m,有![]() 再证
再证![]() 即可.
即可.
(1)因为![]() ,所以
,所以![]() ,
,
令![]() ,
,
所以![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以当![]() 时,
时,![]() 取最大值0.
取最大值0.
所以![]() .
.
即![]() .
.
(2)因为函数![]() 与函数
与函数![]() 有两个不同交点
有两个不同交点![]() ,
,
所以![]() 在
在![]() 上有两个不同的根
上有两个不同的根![]() ,
,![]() ,
,
假设存在![]() ,使得
,使得![]() 在
在![]() 处的切线斜率与
处的切线斜率与![]() 在
在![]() 处的切线斜率相等.
处的切线斜率相等.
所以![]() 有解.
有解.
令![]() ,
,
因为![]() ,所以
,所以![]() 有两个零点,一正一负,设正根为m,有
有两个零点,一正一负,设正根为m,有![]()
当![]() 时,
时,![]() ,即
,即![]() 所以
所以![]() 在
在![]() 上递增,
上递增,
当![]() 时,
时,![]() ,即
,即![]() 所以
所以![]() 在
在![]() 上递减,
上递减,
因为![]() 在
在![]() 上有两个不同的根
上有两个不同的根![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
即存在![]() ,使得
,使得![]() 在
在![]() 处的切线斜率与
处的切线斜率与![]() 在
在![]() 处的切线斜率相等.
处的切线斜率相等.


科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD![]() 中,以D为原点建立空间直角坐标系,E为B
中,以D为原点建立空间直角坐标系,E为B![]() 的中点,F为
的中点,F为![]() 的中点,则下列向量中,能作为平面AEF的法向量的是( )
的中点,则下列向量中,能作为平面AEF的法向量的是( )
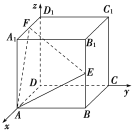
A. (1,-2,4) B. (-4,1,-2)
C. (2,-2,1) D. (1,2,-2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是中国古代的数学专著,其中的“更相减损术”原文是:“可半者半之,不可半者,副置分母、子之数,以少减多,更相减损,求其等也以等数约之”即(如果需要对分数进行约分,那么)可以折半的话,就折半(也就是用2来约分).如果不可以折半的话,那么就比较分母和分子的大小,用大数减去小数,互相减来减去,一直到减数与差相等为止,用这个相等的数字来约分.如图是“更相减损术”的程序框图,如果输入![]() ,
,![]() ,则输出的
,则输出的![]() 值是( )
值是( )
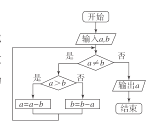
A.72B.70C.34D.36
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,现有4种不同颜色给图中5个区域涂色,要求任意两个相邻区域不同色,共有______种不同涂色方法;若要求4种颜色都用上且任意两个相邻区域不同色,共有______种不同涂色方法.(用数字作答)

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区2007年至2013年农村居民家庭人均纯收入y(单位:千元)的数据如下表:
年 份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
附:回归直线的斜率和截距的最小二乘估计公式分别为:
![]() =
= ,
,![]() =
=![]() -
-![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《汉字听写大会》不断创收视新高,为了避免“书写危机”,弘扬传统文化,某市大约10万名市民进行了汉字听写测试.现从某社区居民中随机抽取50名市民的听写测试情况,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第1组![]() ,第2组
,第2组![]() ,…,第6组
,…,第6组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
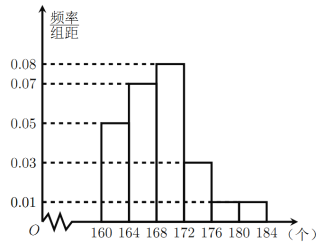
(1)若电视台记者要从抽取的市民中选1人进行采访,求被采访人恰好在第2组或第6组的概率;
(2)试估计该市市民正确书写汉字的个数的众数与中位数;
(3)已知第4组市民中有3名男性,组织方要从第4组中随机抽取2名市同组成弘扬传统文化宣传队,求至少有1名女性市民的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com