
【题目】经过多年的运作,“双十一”抢购活动已经演变成为整个电商行业的大型集体促销盛宴.为迎接2014年“双十一”网购狂欢节,某厂家拟投入适当的广告费,对网上所售产品进行促销.经调查测算,该促销产品在“双十一”的销售量p万件与促销费用x万元满足![]() (其中
(其中![]() ,a为正常数).已知生产该产品还需投入成本
,a为正常数).已知生产该产品还需投入成本![]() 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为
![]() 元/件,假定厂家的生产能力完全能满足市场的销售需求.
元/件,假定厂家的生产能力完全能满足市场的销售需求.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大?
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域是
的定义域是![]() ,且
,且![]() ,
,![]() ,当
,当![]() 时,
时,![]() .
.
(1)判断![]() 的奇偶性,并说明理由;
的奇偶性,并说明理由;
(2)求![]() 在区间
在区间![]() 上的解析式;
上的解析式;
(3)是否存在整数![]() ,使得当
,使得当![]() 时,不等式
时,不等式![]() 有解?证明你的结论.
有解?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点为F,短轴的两个端点分别为A、B,且
的左焦点为F,短轴的两个端点分别为A、B,且![]() ,
,![]() 为等边三角形.
为等边三角形.
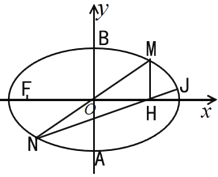
(1)求椭圆C的方程;
(2)如图,点M在椭圆C上且位于第一象限内,它关于坐标原点O的对称点为N;过点M作x轴的垂线,垂足为H,直线![]() 与椭圆C交于另一点J,若
与椭圆C交于另一点J,若![]() ,试求以线段
,试求以线段![]() 为直径的圆的方程;
为直径的圆的方程;
(3)已知![]() 是过点A的两条互相垂直的直线,直线
是过点A的两条互相垂直的直线,直线![]() 与圆
与圆![]() 相交于
相交于![]() 两点,直线
两点,直线![]() 与椭圆C交于另一点R;求
与椭圆C交于另一点R;求![]() 面积取最大值时,直线
面积取最大值时,直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】市场上有一种新型的强力洗衣粉,特点是去污速度快,已知每投放![]() (
(![]() 且
且![]() )个单位的洗衣粉液在一定量水的洗衣机中,它在水中释放的浓度
)个单位的洗衣粉液在一定量水的洗衣机中,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (分钟)变化的函数关系式近似为
(分钟)变化的函数关系式近似为![]() ,其中
,其中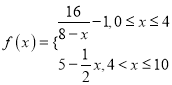 ,若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和,根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起有效去污的作用.
,若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和,根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起有效去污的作用.
(1)若只投放一次4个单位的洗衣液,则有效去污时间可能达几分钟?
(2)若先投放2个单位的洗衣液,6分钟后投放![]() 个单位的洗衣液,要使接下来的4分钟中能够持续有效去污,试求
个单位的洗衣液,要使接下来的4分钟中能够持续有效去污,试求![]() 的最小值(精确到0.1,参考数据:
的最小值(精确到0.1,参考数据: ![]() 取
取![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为梯形,
为梯形, ![]() 底面
底面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.

(1)求证:平面![]()
![]() 平面
平面![]() ;
;
(2)设![]() 为
为![]() 上的一点,满足
上的一点,满足![]() ,若直线
,若直线![]() 与平面
与平面![]() 所成角的正切值为
所成角的正切值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过双曲线![]() 的右支上的一点P作一直线l与两渐近线交于A、B两点,其中P是
的右支上的一点P作一直线l与两渐近线交于A、B两点,其中P是![]() 的中点;
的中点;
(1)求双曲线的渐近线方程;
(2)当P坐标为![]() 时,求直线l的方程;
时,求直线l的方程;
(3)求证:![]() 是一个定值.
是一个定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 前
前![]() 项和为
项和为![]()
(1)若首项![]() ,且对于任意的正整数
,且对于任意的正整数![]() 均有
均有![]() ,(其中
,(其中![]() 为正实常数),试求出数列
为正实常数),试求出数列![]() 的通项公式.
的通项公式.
(2)若数列![]() 是等比数列,公比为
是等比数列,公比为![]() ,首项为
,首项为![]() ,
,![]() 为给定的正实数,满足:①
为给定的正实数,满足:①![]() ,且
,且![]() ②对任意的正整数
②对任意的正整数![]() ,均有
,均有![]() ;试求函数
;试求函数![]() 的最大值(用
的最大值(用![]() 和
和![]() 表示)
表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com