
 sin(
sin(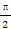 +
+ ).
).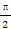 ),2f(2α)+4f(
),2f(2α)+4f(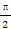 -2α)=1,求f(α)的值.
-2α)=1,求f(α)的值.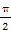 ],单调递增区间为[-
],单调递增区间为[-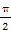 ,0]
,0]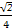
 sin(
sin(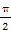 +
+ )
) cos
cos =
= sinx.
sinx.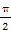 ],单调递增区间为[-
],单调递增区间为[-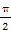 ,0].
,0].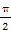 -2α)=1
-2α)=1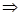 sin2α+2sin(
sin2α+2sin(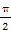 -2α)=1
-2α)=1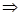 2sinαcosα+2(cos2α-sin2α)=1
2sinαcosα+2(cos2α-sin2α)=1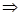 cos2α+2sinαcosα-3sin2α=0
cos2α+2sinαcosα-3sin2α=0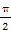 ),
), ,故sinα=
,故sinα=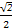 ,
, sinα=
sinα=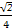 .
.

科目:高中数学 来源:不详 题型:单选题
 ,且
,且 是它的最大值,(其中m、n为常数且
是它的最大值,(其中m、n为常数且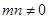 )给出下列命题:①
)给出下列命题:①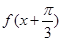 是偶函数;②函数
是偶函数;②函数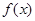 的图象关于点
的图象关于点 对称;③
对称;③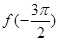 是函数
是函数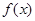 的最小值;④
的最小值;④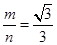 .
.| A.①②③④ | B.②③ | C.①②④ | D.②④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
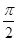 )来表示(x为月份),已知3月份达到最高价9万元,7月份价格最低,为5万元,则国庆节期间的价格约为( )
)来表示(x为月份),已知3月份达到最高价9万元,7月份价格最低,为5万元,则国庆节期间的价格约为( )| A.4.2万元 | B.5.6万元 |
| C.7万元 | D.8.4万元 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
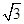 sin x,sin x),b=(cos x,sin x),x∈
sin x,sin x),b=(cos x,sin x),x∈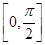 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com