
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切.
相切. ![]() 、
、![]() 是椭圆
是椭圆![]() 的右顶点与上顶点,直线
的右顶点与上顶点,直线![]() 与椭圆相交于
与椭圆相交于![]() 、
、![]() 两点.
两点.

(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)当四边形![]() 面积取最大值时,求
面积取最大值时,求![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.曲线
轴正半轴为极轴,建立极坐标系.曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为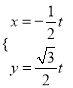 (
(![]() 为参数)
为参数)
(1)求曲线![]() 的直角坐标方程及曲线
的直角坐标方程及曲线![]() 的极坐标方程;
的极坐标方程;
(2)当![]() (
(![]() )时在曲线
)时在曲线![]() 上对应的点为
上对应的点为![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 点的极坐标,并判断
点的极坐标,并判断![]() 是否在曲线
是否在曲线![]() 上(其中点
上(其中点![]() 为半圆的圆心)
为半圆的圆心)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,过点
,过点![]() 且与
且与![]() 轴垂直的直线为
轴垂直的直线为![]() ,
, ![]() 轴,交
轴,交![]() 于点
于点![]() ,直线
,直线![]() 垂直平分
垂直平分![]() ,交
,交![]() 于点
于点![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)记点![]() 的轨迹为曲线
的轨迹为曲线![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于不同两点
交于不同两点![]() ,且
,且![]() (
(![]() 为常数),直线
为常数),直线![]() 与
与![]() 平行,且与曲线
平行,且与曲线![]() 相切,切点为
相切,切点为![]() ,试问
,试问![]() 的面积是否为定值.若为定值,求出
的面积是否为定值.若为定值,求出![]() 的面积;若不是定值,说明理由.
的面积;若不是定值,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的首项为
的首项为![]() ,公差为
,公差为![]() ,等比数列
,等比数列![]() 的首项为
的首项为![]() ,公比为
,公比为![]() .
.
(Ⅰ)若数列![]() 的前
的前![]() 项和
项和![]() ,求
,求![]() ,
, ![]() 的值;
的值;
(Ⅱ)若![]() ,
, ![]() ,且
,且![]() .
.
(i)求![]() 的值;
的值;
(ii)对于数列![]() 和
和![]() ,满足关系式
,满足关系式![]() ,
, ![]() 为常数,且
为常数,且![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
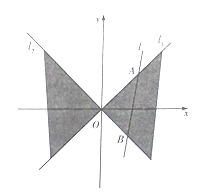
【题目】【2018河南安阳市高三一模】如下图,在平面直角坐标系![]() 中,直线
中,直线![]() 与直线
与直线![]() 之间的阴影部分即为
之间的阴影部分即为![]() ,区域
,区域![]() 中动点
中动点![]() 到
到![]() 的距离之积为1.
的距离之积为1.
(Ⅰ)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)动直线![]() 穿过区域
穿过区域![]() ,分别交直线
,分别交直线![]() 于
于![]() 两点,若直线
两点,若直线![]() 与轨迹
与轨迹![]() 有且只有一个公共点,求证:
有且只有一个公共点,求证: ![]() 的面积恒为定值.
的面积恒为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,射线OA、OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别交OA、OB于A、B两点,当AB的中点C恰好落在直线y=![]() x上时,求直线AB的方程.
x上时,求直线AB的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
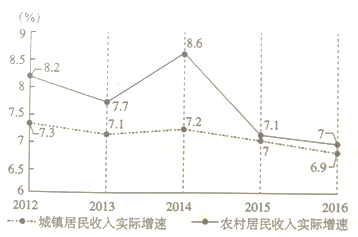
【题目】“砥砺奋进的五年”,首都经济社会发展取得新成就.自2012年以来,北京城乡居民收入稳步增长.随着扩大内需,促进消费等政策的出台,居民消费支出全面增长,消费结构持续优化升级,城乡居民人均可支配收入快速增长,人民生活品质不断提升.下图是北京市2012-2016年城乡居民人均可支配收入实际增速趋势图(例如2012年,北京城镇居民收入实际增速为![]() ,农村居民收入实际增速为
,农村居民收入实际增速为![]() ).
).
(1)从2012-2016五年中任选一年,求城镇居民收入实际增速大于![]() 的概率;
的概率;
(2)从2012-2016五年中任选两年,求至少有一年农村和城镇居民收入实际增速均超过![]() 的概率;
的概率;
(3)由图判断,从哪年开始连续三年农村居民收入实际增速方差最大?(结论不要求证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com