
正方形ABCD中,M为AD的中点,N为AB中点,沿CM、CN分别将三角形CDM和△CBN折起,使CB与CD重合,设B点与D点重合于P,设T为PM的中点,则异面直线CT与PN所成的角为
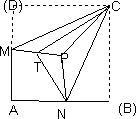
A.30°
B.45°
C.60°
D.90°
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com