
【题目】已知函数f(x)=ax2+(b﹣8)x﹣a﹣ab,当x∈(﹣3,2)时,f(x)>0,当x∈(﹣∞,﹣3)∪(2,+∞)时,f(x)<0.
(1)求f(x)的解析式;
(2)若不等式ax2+bx+c≤0的解集为R,求c的取值范围;
(3)当x>﹣1时,求y= ![]() 的最大值.
的最大值.
【答案】
(1)解:由已知得,方程ax2+(b﹣8)x﹣a﹣ab=0的两个根为﹣3,2,
则 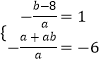 ,即
,即 ![]() ,
,
解得a=﹣3,b=5,
∴f(x)=﹣3x2﹣3x+18
(2)解:由已知得,不等式﹣3x2+5x+c≤0的解集为R,
因为△=52﹣4×(﹣3)×c≤0,
∴c≤﹣ ![]() ,即c的取值范围为(﹣∞,﹣
,即c的取值范围为(﹣∞,﹣ ![]() ]
]
(3)解:y= ![]() =
= ![]() =﹣3×(x+
=﹣3×(x+ ![]() )=﹣3×[(x+1)+
)=﹣3×[(x+1)+ ![]() ﹣1],
﹣1],
因为x>﹣1,(x+1)+ ![]() ≥2,
≥2,
当且仅当x+1= ![]() ,即x=0时取等号,
,即x=0时取等号,
∴当x=0时,ymax=﹣3
【解析】(1)由已知中函数f(x)=ax2+(b﹣8)x﹣a﹣ab,当x∈(﹣3,2)时,f(x)>0,当x∈(﹣∞,﹣3)∪(2,+∞)时,f(x)<0,可得f(x)=0的两根为﹣3,2,由韦达定理(根与系数的关系)我们易求出a,b的值,进而得到函数的解析式;(2)由(1)的结论,根据不等式﹣3x2+5x+c≤0的解集为R,可得△≤0,由此构造关于c的不等式,解不等式即可求出c的取值范围;(3)根据(1)的结论,我们易求出y= ![]() 的解析式,结合基本不等式,分析出函数的值域,即可得到其最大值.
的解析式,结合基本不等式,分析出函数的值域,即可得到其最大值.
【考点精析】本题主要考查了二次函数的性质和解一元二次不等式的相关知识点,需要掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减;求一元二次不等式
上递减;求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边才能正确解答此题.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】在平面四边形ABCD中,AB=BD=CD=1,AB⊥BD,CD⊥BD,将△ABD沿BD折起,使得平面ABD⊥平面BCD,如图. 
(1)求证:AB⊥CD;
(2)若M为AD中点,求直线AD与平面MBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图在三棱锥S﹣ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,SA=SC= ![]() ,M为AB的中点.
,M为AB的中点.
(I)证明:AC⊥SB;
(Ⅱ)求点B到平面SCM的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系并取相同的单位长度,曲线
轴正半轴为极轴建立极坐标系并取相同的单位长度,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)把曲线![]() 的方程化为普通方程,
的方程化为普通方程, ![]() 的方程化为直角坐标方程;
的方程化为直角坐标方程;
(2)若曲线![]() ,
, ![]() 相交于
相交于![]() 两点,
两点, ![]() 的中点为
的中点为![]() ,过点
,过点![]() 做曲线
做曲线![]() 的垂线交曲线
的垂线交曲线![]() 于
于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在四棱锥P﹣ABCD中,底面ABCD是边长为2的正方形,其它四个侧面都是侧棱长为 ![]() 的等腰三角形.
的等腰三角形.
(Ⅰ)求二面角P﹣AB﹣C的大小;
(Ⅱ)在线段AB上是否存在一点E,使平面PCE⊥平面PCD?若存在,请指出点E的位置并证明,若不存在请说明理由.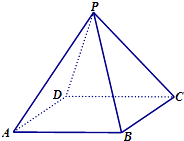
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
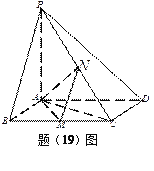
如图,已知四棱锥![]() ,底面
,底面![]() 为菱形,
为菱形,![]() ,
,
![]() ,
, ![]() 平面
平面![]() ,
, ![]() 分别是
分别是![]() 的中点。
的中点。
(1)证明: ![]() ;
;
(2)若![]() 为
为![]() 上的动点,
上的动点,![]() 与平面
与平面![]() 所成最大角
所成最大角
的正切值为![]() ,求二面角
,求二面角![]() 的余弦值。
的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校举行班级篮球赛,某名运动员每场比赛得分记录的茎叶图如下: 
(1)求该运动员得分的中位数和平均数;
(2)估计该运动员每场得分超过10分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极大值点( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的焦距为2,离心率为
的焦距为2,离心率为![]() ,
,![]() 轴上一点
轴上一点![]() 的坐标为
的坐标为![]() .
.
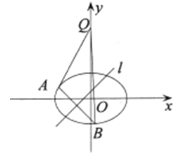
(Ⅰ)求该椭圆的方程;
(Ⅱ)若对于直线![]() ,椭圆
,椭圆![]() 上总存在不同的两点
上总存在不同的两点![]() 与
与![]() 关于直线
关于直线![]() 对称,且
对称,且![]() ,求
,求
实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com