
| A. | -6 | B. | $\sqrt{10}$ | C. | $\sqrt{5}$ | D. | 10 |
分析 根据$\overrightarrow{a},\overrightarrow{b}$的坐标及$\overrightarrow{a}∥\overrightarrow{b}$即可求出x值,从而得出$\overrightarrow{a}$的坐标,进行数量积的坐标运算即可求出$\overrightarrow{a}•\overrightarrow{b}$的值.
解答 解:∵$\overrightarrow{a}∥\overrightarrow{b}$;
∴1•(-4)-2x=0;
∴x=-2;
∴$\overrightarrow{a}=(1,-2),且\overrightarrow{b}=(2,-4)$;
∴$\overrightarrow{a}•\overrightarrow{b}=1×2+(-2)×(-4)=10$.
故选D.
点评 考查平行向量的坐标关系,以及向量数量积的坐标运算.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,3x>0 | B. | ?x0∈R,lgx0=0 | ||
| C. | $?x∈({0,\frac{π}{2}}),x>sinx$ | D. | $?{x_0}∈R,sin{x_0}+cos{x_0}=\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
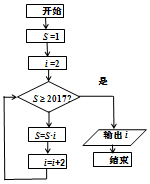
| A. | 使1×2×4×6×…×n≥2017成立的最小整数n | |
| B. | 使1×2×4×6×…×n≥2017成立的最大整数n | |
| C. | 使1×2×4×6×…×n≥2017成立的最小整数n+2 | |
| D. | 使1×2×4×6×…×n≥2017成立的最大整数n+2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
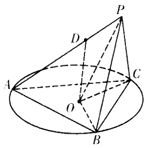 如图所示,正三角形ABC的外接圆半径为2,圆心为O,PB=PC=2,D为AP上一点,AD=2DP,点D在平面ABC内的射影为圆心O.
如图所示,正三角形ABC的外接圆半径为2,圆心为O,PB=PC=2,D为AP上一点,AD=2DP,点D在平面ABC内的射影为圆心O.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com