
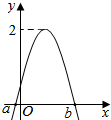 ��ͼ�Ǻ���$f��x��=Asin��2x+ϕ������A��0��|ϕ|��\frac{��}{2}��$ͼ���һ���֣��Բ�ͬ��x1��x2��[a��b]����f��x1��=f��x2������$f��{x_1}+{x_2}��=\sqrt{2}$��������
��ͼ�Ǻ���$f��x��=Asin��2x+ϕ������A��0��|ϕ|��\frac{��}{2}��$ͼ���һ���֣��Բ�ͬ��x1��x2��[a��b]����f��x1��=f��x2������$f��{x_1}+{x_2}��=\sqrt{2}$��������| A�� | f��x����$��-\frac{3��}{8}��\frac{��}{8}��$���������� | B�� | f��x����$��-\frac{3��}{8}��\frac{��}{8}��$���Ǽ����� | ||
| C�� | f��x����$��-\frac{5��}{12}��\frac{��}{12}��$���������� | D�� | f��x����$��-\frac{5��}{12}��\frac{��}{12}��$���Ǽ����� |
���� ����ͼ��ó��Գ���Ϊ��x=$\frac{{x}_{1}+{x}_{2}}{2}$
�������x1+x2=$\frac{��}{2}$-∅��$f��{x_1}+{x_2}��=\sqrt{2}$�����뼴�ɵó�f��x��=2sin��2x$+\frac{��}{4}$��
�������Һ����ĵ����Եó�����ʽ$-\frac{3��}{8}$+k�С�x��$\frac{��}{8}$+k�У�k��z��
�����жϴ𰸣�
��� �⣺���ݺ���ͼ��ó���A=2���Գ���Ϊ��x=$\frac{{x}_{1}+{x}_{2}}{2}$
2sin��x1+x2+∅��=2��x1+x2+∅=$\frac{��}{2}$��x1+x2=$\frac{��}{2}$-∅��
��$f��{x_1}+{x_2}��=\sqrt{2}$��
��2sin��2��$\frac{��}{2}$-∅��+∅��=$\sqrt{2}$��
��sin����-∅��=$\frac{\sqrt{2}}{2}$����|∅|$��\frac{��}{2}$��
��$∅=\frac{��}{4}$
��f��x��=2sin��2x$+\frac{��}{4}$��
��$-\frac{��}{2}$+2k��2x$+\frac{��}{4}$��$\frac{��}{2}$+2k��k��z��
��$-\frac{3��}{8}$+k��x��$\frac{��}{8}$+k��k��z��
��ѡ��A
���� ���⿼�������Ǻ�����ͼ������ʵ����ã��ؼ�������ͼ��ó��Գ��ᣬ��ֵ���ɣ���ǿ�������������ã�


 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��ֱ�Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���������n����β������Ϊn�����7�е�2������22����n�У�n��2����2������$\frac{{n}^{2}-n+2}{2}$��
��ͼ���������n����β������Ϊn�����7�е�2������22����n�У�n��2����2������$\frac{{n}^{2}-n+2}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
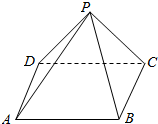 ��֪��������P-ABCD�IJ��ⳤΪ2$\sqrt{3}$��������������εĶ���Ϊ30�㣬���A�����������һ�ܺ�ص�A������·��Ϊ��������
��֪��������P-ABCD�IJ��ⳤΪ2$\sqrt{3}$��������������εĶ���Ϊ30�㣬���A�����������һ�ܺ�ص�A������·��Ϊ��������| A�� | 2$\sqrt{6}$ | B�� | 2$\sqrt{3}$ | C�� | $\sqrt{6}$ | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8 | B�� | $\frac{16}{3}$ | C�� | 3 | D�� | $\frac{8}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | ��1������3������4�� | B�� | ��1������2������3�� | C�� | ��3������4�� | D�� | ��1�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com