
秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数学九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入 ,
, 的值分别为
的值分别为 ,
, ,则输出
,则输出 的值为( )
的值为( )

A. B.
B. C.
C. D.
D.
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源:2017届湖南郴州市高三理第二次质监数学试卷(解析版) 题型:填空题
两所学校分别有2名、3名学生获奖,这5名学生要排成一排合影,则同校学生排在一起的概率是__________.
查看答案和解析>>
科目:高中数学 来源:2017届湖南郴州市高三文第二次质监数学试卷(解析版) 题型:解答题
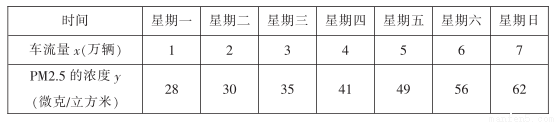
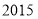 年
年 月,京津冀等地数城市指数“爆表”,北方此轮污染为
月,京津冀等地数城市指数“爆表”,北方此轮污染为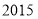 年以来最严重的污染过程.为了探究车流量与
年以来最严重的污染过程.为了探究车流量与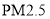 的浓度是否相关,现采集到北方某城市
的浓度是否相关,现采集到北方某城市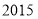 年
年 月份某星期星期一到星期日某一时间段车流量与
月份某星期星期一到星期日某一时间段车流量与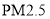 的数据如表:
的数据如表:
(Ⅰ)由散点图知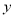 与
与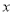 具有线性相关关系,求
具有线性相关关系,求 关于
关于 的线性回归方程;
的线性回归方程;
(Ⅱ)(ⅰ)利用(Ⅰ)所求的回归方程,预测该市车流量为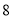 万辆时
万辆时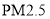 的浓度;
的浓度;
(ⅱ)规定:当一天内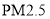 的浓度平均值在
的浓度平均值在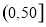 内,空气质量等级为优;当一天内
内,空气质量等级为优;当一天内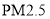 的浓度平均值在
的浓度平均值在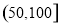 内,空气质量等级为良.为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数.)
内,空气质量等级为良.为使该市某日空气质量为优或者为良,则应控制当天车流量在多少万辆以内?(结果以万辆为单位,保留整数.)
参考公式:回归直线的方程是 ,其中
,其中 ,
, .
.
查看答案和解析>>
科目:高中数学 来源:2017届湖南郴州市高三文第二次质监数学试卷(解析版) 题型:选择题
复数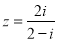 (
(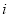 为虚数单位)所对应的点位于复平面内( )
为虚数单位)所对应的点位于复平面内( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
查看答案和解析>>
科目:高中数学 来源:2016-2017年河南漯河高级中学高二理12月月考数学试卷(解析版) 题型:解答题
在 中,角
中,角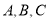 的对边分别为
的对边分别为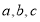 .已知
.已知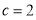 ,向量
,向量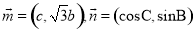 ,且
,且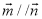 .
.
(1)求角 的大小;
的大小;
(2)若 ,成等差数列,求边
,成等差数列,求边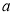 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:2016-2017年安徽滁州部分高中高二理12月联考数学试卷(解析版) 题型:解答题
已知中心在坐标原点 的椭圆
的椭圆 经过点
经过点 ,且点
,且点 为其右焦点.
为其右焦点.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)是否存在平行于 的直线
的直线 ,使得直线
,使得直线 与椭圆
与椭圆 有公共点,且直线
有公共点,且直线 与
与 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com