
【题目】![]() 年上半年,随着新冠肺炎疫情在全球蔓延,全球超过
年上半年,随着新冠肺炎疫情在全球蔓延,全球超过![]() 个国家或地区宣布进人紧急状态,部分国家或地区直接宣布“封国”或“封城”,随着国外部分活动进入停摆,全球经济缺乏活力,一些企业开始倒闭,下表为
个国家或地区宣布进人紧急状态,部分国家或地区直接宣布“封国”或“封城”,随着国外部分活动进入停摆,全球经济缺乏活力,一些企业开始倒闭,下表为![]() 年第一季度企业成立年限与倒闭分布情况统计表:
年第一季度企业成立年限与倒闭分布情况统计表:
企业成立年份 | 2019 | 2018 | 2017 | 2016 | 2015 |
企业成立年限 | 1 | 2 | 3 | 4 | 5 |
倒闭企业数量(万家) | 5.23 | 4.70 | 3.72 | 3.12 | 2.42 |
倒闭企业所占比例 | 21.8% | 19.6% | 15.5% | 13.0% | 10.1% |
根据上表,给出两种回归模型:
模型①:建立曲线型回归模型![]() ,求得回归方程为
,求得回归方程为![]() ;
;
模型②:建立线性回归模型![]() .
.
(1)根据所给的统计量,求模型②中![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)根据下列表格中的数据,比较两种模型的相关指数![]() ,并选择拟合精度更高、更可靠的模型,预测
,并选择拟合精度更高、更可靠的模型,预测![]() 年成立的企业中倒闭企业所占比例(结果保留整数).
年成立的企业中倒闭企业所占比例(结果保留整数).
回归模型 | 模型① | 模型② |
回归方程 |
|
|
|
|
参考公式: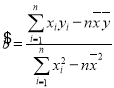 ,
,![]() ;
;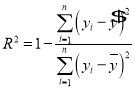 .
.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】我们打印用的A4纸的长与宽的比约为![]() ,之所以是这个比值,是因为把纸张对折,得到的新纸的长与宽之比仍约为
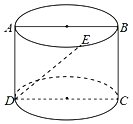
,之所以是这个比值,是因为把纸张对折,得到的新纸的长与宽之比仍约为![]() ,纸张的形状不变.已知圆柱的母线长小于底面圆的直径长(如图所示),它的轴截面ABCD为一张A4纸,若点E为上底面圆上弧AB的中点,则异面直线DE与AB所成的角约为( )
,纸张的形状不变.已知圆柱的母线长小于底面圆的直径长(如图所示),它的轴截面ABCD为一张A4纸,若点E为上底面圆上弧AB的中点,则异面直线DE与AB所成的角约为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在疫情这一特殊时期,教育行政部门部署了“停课不停学”的行动,全力帮助学生在线学习.复课后进行了摸底考试,某校数学教师为了调查高三学生这次摸底考试的数学成绩与在线学习数学时长之间的相关关系,对在校高三学生随机抽取45名进行调查.知道其中有25人每天在线学习数学的时长是不超过1小时的,得到了如下的等高条形图:
(1)是否有![]() 的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”;
的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”;
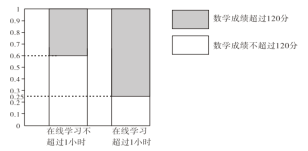
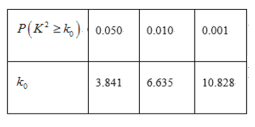
(2)将频率视为概率,从全校高三学生这次数学成绩超过120分的学生中随机抽取10人,求抽取的10人中每天在线学习时长超过1小时的人数的数学期望与方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 与抛物线
与抛物线![]() 有共同的焦点
有共同的焦点![]() ,且两曲线的公共点到
,且两曲线的公共点到![]() 的距离是它到直线
的距离是它到直线![]() (点
(点![]() 在此直线右侧)的距离的一半.
在此直线右侧)的距离的一半.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,直线
为坐标原点,直线![]() 过点
过点![]() 且与椭圆交于
且与椭圆交于![]() 两点,以
两点,以![]() 为邻边作平行四边形
为邻边作平行四边形![]() .是否存在直线
.是否存在直线![]() ,使点
,使点![]() 落在椭圆
落在椭圆![]() 或抛物线
或抛物线![]() 上?若存在,求出点
上?若存在,求出点![]() 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,直线
,直线![]() 不过原点
不过原点![]() 且不平行于坐标轴,
且不平行于坐标轴,![]() 与
与![]() 有两个交点
有两个交点![]() ,
,![]() ,线段
,线段![]() 的中点为
的中点为![]() .
.
(1)若![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上,![]() 、
、![]() 分别为椭圆的两个焦点,求
分别为椭圆的两个焦点,求![]() 的范围;
的范围;
(2)若![]() 过点
过点![]() ,射线
,射线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,四边形
,四边形![]() 能否为平行四边形?若能,求此时直线
能否为平行四边形?若能,求此时直线![]() 斜率;若不能,说明理由.
斜率;若不能,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点
的中点![]() 是由
是由![]() 绕直线
绕直线![]() 旋转得到,连结
旋转得到,连结![]() ,
,![]() ,
,![]() .
.
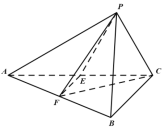
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,棱
,棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com