
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() .
.
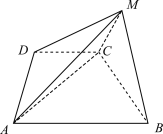
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)在棱![]() 上是否存在一点E,使得二面角
上是否存在一点E,使得二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)证明见解析(2)证明见解析(3)存在;![]()
【解析】
(1)由线面平行判定定理证明即可;
(2)由勾股定理得出![]() ,进而得
,进而得![]() ,再由面面垂直的性质定理即可证明
,再由面面垂直的性质定理即可证明![]() 平面
平面![]() ;
;
(3)建立空间直角坐标系,利用向量法求解即可.
证明:(1)因为![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)取![]() 的中点N,连接
的中点N,连接![]() .
.
在直角梯形![]() 中,
中,
易知![]() ,且
,且![]() .
.
在![]() 中,由勾股定理得
中,由勾股定理得![]() .
.
在![]() 中,由勾股定理逆定理可知
中,由勾股定理逆定理可知![]() .
.
又因为平面![]() 平面
平面![]() ,
,
且平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
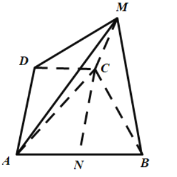
(3)取![]() 的中点O,连接
的中点O,连接![]() ,
,![]() .
.
所以![]() ,
,
因为![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() ,
,
所以![]() .
.
如图建立空间直角坐标系![]() ,
,

则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
易知平面![]() 的一个法向量为
的一个法向量为![]() .
.
假设在棱![]() 上存在一点E,使得二面角
上存在一点E,使得二面角![]() 的大小为
的大小为![]() .
.
不妨设![]() (
(![]() ),
),
所以![]() ,
,
设![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
则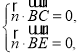 即
即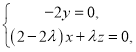
令![]() ,
,![]() ,所以
,所以![]() .
.
从而 .
.
解得![]() 或
或![]() .
.
因为![]() ,所以
,所以![]() .
.
由题知二面角![]() 为锐二面角.
为锐二面角.
所以在棱![]() 上存在一点E,使得二面角
上存在一点E,使得二面角![]() 的大小为
的大小为![]() ,
,
此时![]() .
.


科目:高中数学 来源: 题型:
【题目】科技创新能力是决定综合国力和国际竞争力的关键因素,也是推动经济实现高质量发展的重要支撑,而研发投入是科技创新的基本保障,下图是某公司从2010年到2019年这10年研发投入的数据分布图:

其中折线图是该公司研发投入占当年总营收的百分比,条形图是当年研发投入的数值(单位:十亿元).
(I)从2010年至2019年中随机选取一年,求该年研发投入占当年总营收的百分比超过10%的概率;
(II)从2010年至2019年中随机选取两个年份,设X表示其中研发投入超过500亿元的年份的个数,求X的分布列和数学期望;
(III)根据图中的信息,结合统计学知识,判断该公司在发展的过程中是否比较重视研发,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国著名数学家华罗庚先生曾说:数缺形时少直观,形缺数时难入微,数形结合百般好,隔裂分家万事休.在数学的学习和研究中,常用函数的图象研究函数的性质,也常用函数的解析式来琢磨函数的图象特征.如函数![]() 的图象大致为( )
的图象大致为( )
A. B.
B.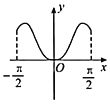
C.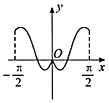 D.
D.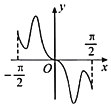
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(1)求函数![]() 的极值点;
的极值点;
(2)定义:若函数![]() 的图像与直线
的图像与直线![]() 有公共点,我们称函数
有公共点,我们称函数![]() 有不动点.这里取:
有不动点.这里取:![]() ,若
,若![]() ,如果函数
,如果函数![]() 存在不动点,求实数
存在不动点,求实数![]() 取值范围.
取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
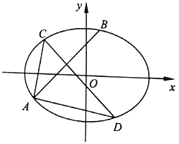
【题目】如图,在平面直角坐标系![]() 中,椭圆
中,椭圆![]() :
:![]() 过点
过点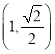 ,且椭圆的离心率为
,且椭圆的离心率为![]() ,直线
,直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中垂线交椭圆
的中垂线交椭圆![]() 于
于![]() 、
、![]() 两点.
两点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)求线段![]() 长的最大值;
长的最大值;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )


A. 2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件
B. 2018年1~4月的业务量同比增长率均超过50%,在3月底最高
C. 从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致
D. 从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1),在矩形![]() 中,
中,![]() ,
,![]() 在边
在边![]() 上,
上,![]() .沿
.沿![]() ,
,![]() 将
将![]() 和
和![]() 折起,使平面
折起,使平面![]() 和平面
和平面![]() 都与平面
都与平面![]() 垂直,如图(2).
垂直,如图(2).
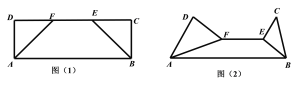
(1)试判断图(2)中直线![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)求平面![]() 和平面
和平面![]() 所成锐角二面角的余弦值.
所成锐角二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列四个结论:
,给出下列四个结论:
①函数![]() 的最小正周期是
的最小正周期是![]() ;
;
②函数![]() 在区间
在区间![]() 上是减函数;
上是减函数;
③函数![]() 的图象关于直线
的图象关于直线![]() 对称;
对称;
④函数![]() 的图象可由函数
的图象可由函数![]() 的图象向左平移
的图象向左平移![]() 个单位得到其中所有正确结论的编号是( )
个单位得到其中所有正确结论的编号是( )
A.①②B.①③C.①②③D.①③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:在长方体![]() 中,
中,![]() ,点
,点![]() 是线段
是线段![]() 上的一个动点,则①
上的一个动点,则①![]() 的最小值等于__________;②直线
的最小值等于__________;②直线![]() 与平面
与平面![]() 所成角的正切值的取值范围为____________.
所成角的正切值的取值范围为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com