
【题目】已知函数![]() .
.
(1)当![]() 时,求证:对
时,求证:对![]() 时,
时, ![]() ;
;
(2)当![]() 时,讨论函数
时,讨论函数![]() 零点的个数.
零点的个数.
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)函数求导![]() ,再求导得
,再求导得![]() 恒成立,又因为
恒成立,又因为![]() 恒成立;
恒成立;
(2)由(1)可知,当x≤0时,f″(x)≤0,可得 对x∈R,f′(x)≥0,即ex≥x+1,分类讨论当x≥-1时,当x<-1时,函数y=f(x)的零点个数即可得解;
当x<-1时,再分0≤m≤1和m<0两种情况进行讨论,由函数零点定理进行判断即可得到答案.
试题解析:,所以
(1)当![]() 时,
时, ![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,当
,当![]() 时,
时, ![]() ,即
,即![]() ,所以函数
,所以函数![]() 在
在![]() 上为增函数,即当
上为增函数,即当![]() 时,
时, ![]() ,所以当
,所以当![]() 时,
时, ![]() 恒成立,所以函数
恒成立,所以函数![]() 在
在![]() 上为增函数,又因为
上为增函数,又因为![]() ,所以当
,所以当![]() 时,对
时,对![]() 恒成立.
恒成立.
(2)由(1)知,当![]() 时,
时, ![]() ,所以
,所以![]() ,所以函数
,所以函数![]() 的减区间为
的减区间为![]() ,增函数为
,增函数为![]() .所以
.所以![]() ,所以对
,所以对![]()
![]() ,
, ![]() ,即
,即![]() .
.
①当![]() 时,
时, ![]() ,又
,又![]() ,
, ![]() ,即
,即![]() ,所以当
,所以当![]() 时,函数
时,函数![]() 为增函数,又
为增函数,又![]() ,所以当
,所以当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上有且仅有一个零点,且为
上有且仅有一个零点,且为![]() .
.
②当![]() 时,(ⅰ)当
时,(ⅰ)当![]() 时,
时, ![]() ,所以
,所以![]() ,所以函数
,所以函数![]() 在
在![]() 上递增,所以
上递增,所以![]() ,且
,且![]() ,故
,故![]() 时,函数
时,函数![]() 在区间
在区间![]() 上无零点.
上无零点.
(ⅱ)当![]() 时,
时, ![]() ,令
,令![]() ,则
,则![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增,
上单调递增, ![]() ,当
,当![]() 时,
时, 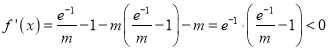 ,又曲线
,又曲线![]() 在区间
在区间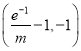 上不间断,所以
上不间断,所以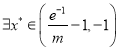 ,使
,使![]() ,故当
,故当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,所以函数
,所以函数![]() 的减区间为
的减区间为![]() ,增区间为
,增区间为![]() ,又
,又![]() ,所以对
,所以对![]() ,又当
,又当![]() 时,
时, ![]() ,又
,又![]() ,曲线
,曲线![]() 在区间
在区间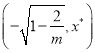 上不间断.所以
上不间断.所以![]() ,且唯一实数
,且唯一实数![]() ,使得
,使得![]() ,综上,当
,综上,当![]() 时,函数
时,函数![]() 有且仅有一个零点;当
有且仅有一个零点;当![]() 时,函数
时,函数![]() 有个两零点.
有个两零点.


科目:高中数学 来源: 题型:
【题目】在参加市里主办的科技知识竞赛的学生中随机选取了40名学生的成绩作为样本,这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组:第一组,成绩大于等于40分且小于50分;第二组,成绩大于等于50分且小于60分;……第六组,成绩大于等于90分且小于等于100分,据此绘制了如图所示的频率分布直方图.在选取的40名学生中.

(1)求成绩在区间![]() 内的学生人数及成绩在区间
内的学生人数及成绩在区间![]() 内平均成绩;
内平均成绩;
(2)从成绩大于等于80分的学生中随机选3名学生,求至少有1名学生成绩在区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x2﹣4x+a,g(x)=logax(a>0且a≠1).
(1)若函数f(x)在[﹣1,3m]上不具有单调性,求实数m的取值范围;
(2)若f(1)=g(1)
①求实数a的值;
②设t1= ![]() f(x),t2=g(x),t3=2x , 当x∈(0,1)时,试比较t1 , t2 , t3的大小.
f(x),t2=g(x),t3=2x , 当x∈(0,1)时,试比较t1 , t2 , t3的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前项和为Sn , 且a2=2,S5=15,数列{bn}的前项和为Tn , 且b1= ![]() ,2nbn+1=(n+1)bn(n∈N*)
,2nbn+1=(n+1)bn(n∈N*)
(Ⅰ)求数列{an}通项公式an及前项和Sn;
(Ⅱ) 求数列{bn}通项公式bn及前项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司制定了一个激励销售人员的奖励方案:当销售利润不超过8万元时,按销售利润的15%进行奖励;当销售利润超过8万元时,若超出A万元,则超出部分按log5(2A+1)进行奖励.记奖金为y(单位:万元),销售利润为x(单位:万元).
(1)写出奖金y关于销售利润x的关系式;
(2)如果业务员小江获得3.2万元的奖金,那么他的销售利润是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A,B,C所对的边分别为a,b,c,若bcosC+ccosB=asinA,则△ABC的形状为( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣2x﹣8,g(x)=2x2﹣5x﹣18
(1)求不等式g(x)<0的解集
(2)若对一切x>2,均有f(x)≥(m+2)x﹣m﹣15成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知命题p:方程 ![]() 表示焦点在y轴的椭圆;命题q:关于x的不等式x2﹣2x+m>0的解集是R; 若“p∧q”是假命题,“p∨q”是真命题,求实数m的取值范围.
表示焦点在y轴的椭圆;命题q:关于x的不等式x2﹣2x+m>0的解集是R; 若“p∧q”是假命题,“p∨q”是真命题,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(Ⅲ)若这100名学生语文成绩某些分数段的人数(![]() )与数学成绩相应分数段的人数(
)与数学成绩相应分数段的人数(![]() )之比如表所示,求数学成绩在
)之比如表所示,求数学成绩在![]() 之外的人数.
之外的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com