
有一种新型的洗衣液,去污速度特别快.已知每投放k(1≤k≤4,且k∈R)个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度y(克/升)随着时间x(分钟)变化的函数关系式近似为y=k·f(x),其中f(x)= 若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.
若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.
(1)若只投放一次k个单位的洗衣液,两分钟时水中洗衣液的浓度为3(克/升),求k的值;
(2)若只投放一次4个单位的洗衣液,则有效去污时间可达几分钟?
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题2第3课时练习卷(解析版) 题型:填空题
在△ABC中,∠B=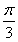 ,O为△ABC的外心,P为劣弧AC上一动点,且
,O为△ABC的外心,P为劣弧AC上一动点,且 =x
=x  +y
+y  (x,y∈R),则x+y的取值范围为________.
(x,y∈R),则x+y的取值范围为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第6课时练习卷(解析版) 题型:解答题
已知函数f(x)= m(x-1)2-2x+3+ln x,m≥1.
m(x-1)2-2x+3+ln x,m≥1.
(1)当m= 时,求函数f(x)在区间[1,3]上的极小值;
时,求函数f(x)在区间[1,3]上的极小值;
(2)求证:函数f(x)存在单调递减区间[a,b];
(3)是否存在实数m,使曲线C:y=f(x)在点P(1,1)处的切线l与曲线C有且只有一个公共点?若存在,求出实数m的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第4课时练习卷(解析版) 题型:解答题
首届世界低碳经济大会在南昌召开,本届大会以“节能减排,绿色生态”为主题.某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为y=x2-200x+80 000,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第4课时练习卷(解析版) 题型:选择题
若点(x,y)位于曲线y=|x|与y=2所围成的封闭区域,则2x-y的最小值是( )
A.-6 B.-2
C.0 D.2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第3课时练习卷(解析版) 题型:选择题
若定义在R上的偶函数f(x)满足f(x+2)=f(x),且x∈[0,1]时,f(x)=x,则方程f(x)=log3|x|的解有( )
A.2个 B.3个
C.4个 D.多于4个
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第2课时练习卷(解析版) 题型:解答题
已知函数f(x)=x2+ (x≠0,a∈R).
(x≠0,a∈R).
(1)判断函数f(x)的奇偶性;
(2)若f(x)在区间[2,+∞)上是增函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试专题1第1课时练习卷(解析版) 题型:选择题
已知命题p:x2+2x-3>0;命题q:x>a,且?q的一个充分不必要条件是?p,则a的取值范围是( )
A.a≥1 B.a≤1
C.a≥-1 D.a≤-3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学理复习方案二轮作业手册新课标·通用版专题八练习卷(解析版) 题型:解答题
已知直线l1:4x-3y+6=0和直线l2:x=-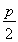 (p>2).若拋物线C:y2=2px上的点到直线l1和直线l2的距离之和的最小值为2.
(p>2).若拋物线C:y2=2px上的点到直线l1和直线l2的距离之和的最小值为2.
(1)求抛物线C的方程;
(2)若拋物线上任意一点M处的切线l与直线l2交于点N,试问在x轴上是否存在定点Q,使Q点在以MN为直径的圆上,若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com