
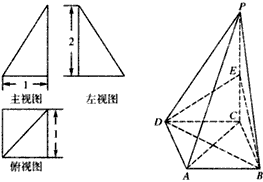
科目:高中数学 来源: 题型:
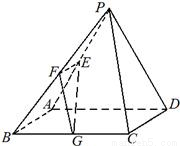
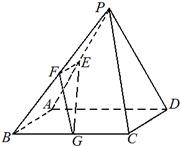 已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PA、PB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E、F、G分别是PA、PB、BC的中点.
| ||
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源:2014届江西省景德镇市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
已知正四棱锥P—ABCD的四条侧棱,底面四条边及两条对角线共10条线段,现有一只蚂蚁沿着这10条线段从一个顶点爬行到另一个顶点,规定: (1)从一个顶点爬行到另一个顶点视为一次爬行;(2)从任一顶点向另4个顶点爬行是等可能的(若蚂蚁爬行在底面对角线上时仍按原方向直行). 则蚂蚁从顶点P开始爬行4次后恰好回到顶点P的概率是( )
A.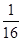 B.
B. C.
C.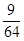 D.
D.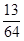
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省温州市瓯海中学高三(上)第一次月考数学试卷(理科)(解析版) 题型:解答题
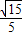 ?
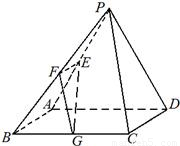
?
查看答案和解析>>
科目:高中数学 来源:2010年辽宁省丹东市高考数学二模试卷(理科)(解析版) 题型:解答题
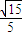 ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com