
【题目】已知![]() ,
,
(1)求![]() 的单调递增区间;
的单调递增区间;
(2)若函数![]() 在
在![]() 上只有一个零点,求实数
上只有一个零点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)(-![]() ,-1)和(
,-1)和(![]() ,+∞)(2)
,+∞)(2)![]() -2ln 2≤a<2ln 3-2或a=2ln 2-1.
-2ln 2≤a<2ln 3-2或a=2ln 2-1.
【解析】
(1)f(x)的定义域为{x|x≠-1}.
∵f(x)=x2-2x-ln(x+1)2,∴f′(x)=2x-2-![]() =
=![]() ,
,
解![]() 得-
得-![]() <x<-1或x>
<x<-1或x>![]() ,
,
∴f(x)的单调递增区间是(-![]() ,-1)和(
,-1)和(![]() ,+∞).
,+∞).
(2)由已知得F(x)=x-ln(x+1)2+a,且x≠-1,∴F′(x)=1-![]() =
=![]() .
.
∴当x<-1或x>1时,F′(x)>0;当-1<x<1时,F′(x)<0.
∴当-![]() <x<1时,F′(x)<0,此时,F(x)单调递减;
<x<1时,F′(x)<0,此时,F(x)单调递减;
当1<x<2时,F′(x)>0,此时,F(x)单调递增.
∵F![]() =-
=-![]() +2ln 2+a>a,F(2)=2-2ln 3+a<a,∴F
+2ln 2+a>a,F(2)=2-2ln 3+a<a,∴F![]() >F(2).
>F(2).
∴F(x)在![]() 上只有一个零点
上只有一个零点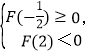 或F(1)=0.
或F(1)=0.
由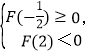 得
得![]() -2ln 2≤a<2ln 3-2;
-2ln 2≤a<2ln 3-2;
由F(1)=0得a=2ln 2-1.
∴实数a的取值范围为![]() -2ln 2≤a<2ln 3-2或a=2ln 2-1.
-2ln 2≤a<2ln 3-2或a=2ln 2-1.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(x+a)﹣x,a∈R.
(1)当a=﹣1时,求f(x)的单调区间;
(2)若x≥1时,不等式ef(x)+ ![]() x2>1恒成立,求实数a的取值范围.
x2>1恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,C是以AB为直径的圆O上异于A,B的点,平面PAC⊥平面ABC,PA=PC=AC=2,BC=4,E,F 分别是PC,PB的中点,记平面AEF与平面ABC的交线为直线l.
(Ⅰ)求证:直线l⊥平面PAC;
(Ⅱ)直线l上是否存在点Q,使直线PQ分别与平面AEF、直线EF所成的角互余?若存在,求出|AQ|的值;若不存在,请说明理由.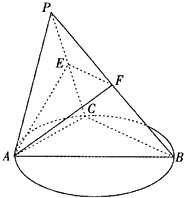
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 已知函数f(x)=ax3+bx2的图象经过点M(1,4),曲线在点M处的切线恰好与直线x+9y﹣3=0垂直.
(1)求实数a、b的值
(2)若函数f(x)在区间[m,m+1]上单调递增,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣2a|+|x+ ![]() |
|
(1)当a=1时,求不等式f(x)>4的解集;
(2)若不等式f(x)≥m2﹣m+2 ![]() 对任意实数x及a恒成立,求实数m的取值范围.
对任意实数x及a恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现从某高中随机抽取部分高二学生,调査其到校所需的时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中到校所需时间的范围是![]() ,样本数据分组为
,样本数据分组为![]() .
.

(1)求直方图中![]() 的值;
的值;
(2)如果学生到校所需时间不少于1小时,则可申请在学校住宿.若该校录取1200名新生,请估计高二新生中有多少人可以申请住宿;
(3)以直方图中的频率作为概率,现从该学校的高二新生中任选4名学生,用![]() 表示所选4名学生中“到校所需时间少于40分钟”的人数,求
表示所选4名学生中“到校所需时间少于40分钟”的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足 ![]() (其中a>0,a≠1)
(其中a>0,a≠1)
(Ⅰ)求f(x)的表达式;
(Ⅱ)对于函数f(x),当x∈(﹣1,1)时,f(1﹣m)+f(1﹣m2)<0,求实数m的取值范围;
(Ⅲ)当x∈(﹣∞,2)时,f(x)﹣4的值为负数,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com