Question

12．已知点P是边长为4的正方形内任一点，则点P到四个顶点的距离均大于2的概率是1$-\frac{π}{4}$．

Answer 1

分析 根据题意，先求出满足条件的正方形ABCD的面积，再求出满足条件正方形内的点到正方形的顶点A、B、C、D的距离均不小于2的图形的面积，然后代入几何概型公式即可得到答案．

解答 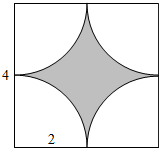解：满足条件的正方形ABCD如下图所示：
其中正方形的面积S_正方形=4×4=16；
满足到正方形的顶点A、B、C、D的距离均不小于2的平面区域如图中阴影部分所示
则S_阴影=16-4π，
故该正方形内的点到正方形的顶点A、B、C、D的距离均不小于1的概率是P=$\frac{{S}_{阴影}}{{S}_{正方形}}$=$\frac{16-4π}{16}$=1$-\frac{π}{4}$；
故答案为：1$-\frac{π}{4}$．

点评 本题考查几何概型的计算，解题的关键理解几何概型的意义，即将长度、面积、体积的比值转化为事件发生的概率