
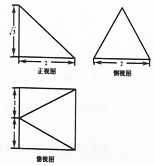
 某几何体的三视图如图所示(单位:cm),则该几何体的体积是$\frac{4\sqrt{3}}{3}$(单位:cm3),表面积是8+$\sqrt{3}$+$\sqrt{7}$(单位:cm2)
某几何体的三视图如图所示(单位:cm),则该几何体的体积是$\frac{4\sqrt{3}}{3}$(单位:cm3),表面积是8+$\sqrt{3}$+$\sqrt{7}$(单位:cm2) 分析 由已知中的三视图可得:该几何体是一个以俯视图为底面的四棱锥,代入棱锥体积公式和表面积公式,可得答案.
解答 解:由已知中的三视图可得:该几何体是一个以俯视图为底面的四棱锥,
其直观图如下图所示: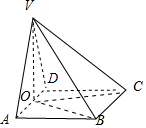
底面ABCD的面积为:2×2=4cm2,
高VO=$\sqrt{3}$cm,
故该几何体的体积V=$\frac{4\sqrt{3}}{3}$cm3,
侧面VAD的面积为:$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$cm2,
VA=VD=2cm,
OB=OC=$\sqrt{5}$cm,VB=VC=2$\sqrt{2}$cm,
侧面VAB和侧面BCD的面积为:$\frac{1}{2}$×2×2=2cm2,
侧面VBC底面上的高为$\sqrt{7}$cm,
故侧面VBC的面积为:$\frac{1}{2}$×2×$\sqrt{7}$=$\sqrt{7}$cm2,
故几何体的表面积S=4+$\sqrt{3}$+2×2+$\sqrt{7}$=8+$\sqrt{3}$+$\sqrt{7}$cm2,
故答案为:$\frac{4\sqrt{3}}{3}$,8+$\sqrt{3}$+$\sqrt{7}$
点评 本题考查的知识点是棱柱的体积和表面积,棱锥的体积和表面积,简单几何体的三视图,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,sinx<0 | B. | ?x∈R,sinx≤0 | C. | ?x∈R,sinx≤0 | D. | ?x∈R,sinx<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
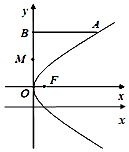 已知抛物线y2=2px(p>0)的焦点F与双曲线4x2-12y2=3的右焦点重合,A是抛物线上横坐标为4,且位于x轴上方的点,过A作AB垂直M于y轴,垂足为B.OB的中点为M
已知抛物线y2=2px(p>0)的焦点F与双曲线4x2-12y2=3的右焦点重合,A是抛物线上横坐标为4,且位于x轴上方的点,过A作AB垂直M于y轴,垂足为B.OB的中点为M查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com