
【题目】中石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了部分儿口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探. 由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用.勘探初期数据资料见如表:

(Ⅰ)1~6号旧井位置线性分布,借助前5组数据求得回归直线方程为![]() ,求
,求![]() ,并估计
,并估计![]() 的预报值;
的预报值;
(Ⅱ)现准备勘探新井![]() ,若通过1、3、5、7号井计算出的
,若通过1、3、5、7号井计算出的![]() 的值(
的值(![]() 精确到0.01)相比于(Ⅰ)中
精确到0.01)相比于(Ⅰ)中![]() 的值之差不超过10%,则使用位置最接近的已有旧井
的值之差不超过10%,则使用位置最接近的已有旧井![]() ,否则在新位置打开,请判断可否使用旧井?
,否则在新位置打开,请判断可否使用旧井?
(参考公式和计算结果: )
)
(Ⅲ)设出油量与勘探深度的比值![]() 不低于20的勘探并称为优质井,那么在原有井号1~6的出油量不低于50L的井中任意勘探3口井,求恰好2口是优质井的概率.
不低于20的勘探并称为优质井,那么在原有井号1~6的出油量不低于50L的井中任意勘探3口井,求恰好2口是优质井的概率.
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() 的离心率是
的离心率是![]() ,
,![]() ,
,![]() 分别为椭圆E的左右顶点,B为上顶点,
分别为椭圆E的左右顶点,B为上顶点,![]() 的面积为
的面积为![]() 直线l过点
直线l过点![]() 且与椭圆E交于P,Q两点.
且与椭圆E交于P,Q两点.

![]() 求椭圆E的标准方程;
求椭圆E的标准方程;
![]() 求
求![]() 面积的最大值;
面积的最大值;
![]() 设直线
设直线![]() 与直线
与直线![]() 交于点N,证明:点N在定直线上,并写出该直线方程.
交于点N,证明:点N在定直线上,并写出该直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 和动点
和动点![]() ,以线段
,以线段![]() 为直径的圆内切于圆
为直径的圆内切于圆![]() .
.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)已知点![]() ,
, ![]() ,经过点
,经过点![]() 的直线
的直线![]() 与动点
与动点![]() 的轨迹交于
的轨迹交于![]() ,
, ![]() 两点,求证:直线
两点,求证:直线![]() 与直线
与直线![]() 的斜率之和为定值.
的斜率之和为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据说伟大的阿基米德逝世后,敌军将领马塞拉斯给他建了一块墓碑,在墓碑上刻了一个如图所示的图案,图案中球的直径、圆柱底面的直径和圆柱的高相等,圆锥的顶点为圆柱上底面的圆心,圆锥的底面是圆柱的下底面.

(1)试计算出图案中圆柱与球的体积比;
(2)假设球半径![]() .试计算出图案中圆锥的体积和表面积.
.试计算出图案中圆锥的体积和表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:极坐标与参数方程
在平面直角坐标系![]() 中,将曲线
中,将曲线![]() (
(![]() 为参数) 上任意一点
为参数) 上任意一点![]() 经过伸缩变换
经过伸缩变换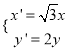 后得到曲线
后得到曲线![]() 的图形.以坐标原点
的图形.以坐标原点![]() 为极点,x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,已知直线
为极点,x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(Ⅰ)求曲线![]() 和直线
和直线![]() 的普通方程;
的普通方程;
(Ⅱ)点P为曲线![]() 上的任意一点,求点P到直线
上的任意一点,求点P到直线![]() 的距离的最大值及取得最大值时点P的坐标.
的距离的最大值及取得最大值时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学在生物研究性学习中,对春季昼夜温差大小与黄豆种子发芽多少之间的关系进行研究,于是他在4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天每100颗种子浸泡后的发芽数,得到如下资料:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差 | 10 | 11 | 13 | 12 | 8 |
发芽数 | 23 | 25 | 30 | 26 | 16 |
(1)从这5天中任选2天,求这2天发芽的种子数均不小于25的概率;
(2)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另三天的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
附:回归直线的斜率和截距的最小二乘估计公式分别为 ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,过
,过![]() 任作一条与坐标轴都不垂直的直线,与
任作一条与坐标轴都不垂直的直线,与![]() 交于
交于![]() 两点,且
两点,且![]() 的周长为
的周长为![]() .当直线
.当直线![]() 的斜率为
的斜率为![]() 时,
时,![]() 与
与![]() 轴垂直
轴垂直
(1)求椭圆![]() 的方程
的方程
(2)若![]() 是该椭圆上位于第一象限的一点,过
是该椭圆上位于第一象限的一点,过![]() 作圆
作圆![]() 的切线,切点为
的切线,切点为![]() ,求
,求![]() 的值;
的值;
(3)设![]() 为定点,直线
为定点,直线![]() 过点
过点![]() 与
与![]() 轴交于点
轴交于点![]() ,且与椭圆交于
,且与椭圆交于![]() 两点,设
两点,设![]() ,
,![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() (
(![]() ,
,![]() )的部分图象如图中实线所示,图中圆C与
)的部分图象如图中实线所示,图中圆C与![]() 的图象交于M,N两点,且M在y轴上,则下列说法中正确的是( )
的图象交于M,N两点,且M在y轴上,则下列说法中正确的是( )

A.函数![]() 的最小正周期是2π
的最小正周期是2π
B.函数![]() 的图象关于点
的图象关于点![]() 成中心对称
成中心对称
C.函数![]() 在
在![]() 单调递增
单调递增
D.将函数![]() 的图象向左平移
的图象向左平移![]() 后得到的关于y轴对称
后得到的关于y轴对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com