
【题目】已知椭圆![]() :
:![]() (
(![]() )的离心率为
)的离心率为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,且椭圆
,且椭圆![]() 上任意一点到
上任意一点到![]() 点的最大距离为
点的最大距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,点
两点,点![]() 为椭圆
为椭圆![]() 长轴上的一点,求
长轴上的一点,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用椭圆的离心率可以求得![]() ,利用
,利用![]() 的最大值求出
的最大值求出![]() 的值,即可求得椭圆
的值,即可求得椭圆![]() 的标准方程;
的标准方程;
(2)联立直线方程与椭圆方程,为避免直线方程斜率是否存在的讨论,可设直线方程为![]() ,先求
,先求![]() ,
,![]() 两点间距离,再求点
两点间距离,再求点![]() 到直线的距离,即可求面积,因为面积
到直线的距离,即可求面积,因为面积![]() 由底和高两部分构成,所以分别求出两部分的最大值,即可求出面积
由底和高两部分构成,所以分别求出两部分的最大值,即可求出面积![]() 的最大值.
的最大值.
(1)解法一:由题意可得离心率![]() ,
,
又![]() ,∴
,∴![]() ,
,![]() ,
,
令点![]() 为椭圆
为椭圆![]() 上任意一点,
上任意一点,
则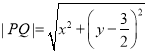
![]()
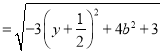
![]() ,
,
∴![]() ,∴
,∴![]() ,
,![]() ,
,
∴椭圆![]() 的标准方程为
的标准方程为![]() .
.
解法二:由题意可得离心率![]() ,
,
又![]() ,∴
,∴![]() ,
,![]() ,
,
令椭圆上任意一点![]() ,
,
![]()
![]()
![]()
![]() ,
,
当![]() 时,
时,![]() ,
,
![]()
![]() ,满足
,满足![]() ;
;
当![]() 时,
时,![]() ,
,
解得![]() (负值舍去),
(负值舍去),![]() ,
,
则![]() ,不满足条件,舍去,
,不满足条件,舍去,
综上,![]() ,
,![]() ,
,
椭圆![]() 的标准方程为
的标准方程为![]() ;
;
(2)设![]() 点坐标为
点坐标为![]() (
(![]() ),
),
直线![]() 的方程为
的方程为![]() ,联立直线方程与椭圆方
,联立直线方程与椭圆方
程化简得![]() ,
,
令![]() ,
,![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,
,
由韦达定理可得![]() ,
,![]() ,
,
则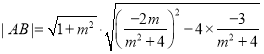 ,
,
化简得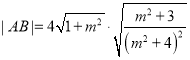 ,
,
点![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
![]()
![]() 的面积
的面积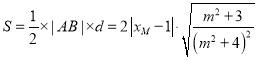 ,
,
令![]() ,
,
则![]()
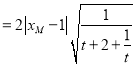 ,
,
当![]() 时,
时,![]() ,
,
当且仅当![]() ,
,![]() 时等号成立,
时等号成立,
此时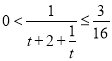 ,
,![]()
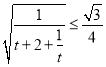 ,
,
![]()
![]() ,
,
![]() 当且仅当
当且仅当![]() 时,
时,![]() 取到最大值为
取到最大值为![]() ,此时
,此时![]() 面积
面积![]() 取到最大值,
取到最大值,
即![]() ,此时直线
,此时直线![]() 的方程为
的方程为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
综上,![]() 面积的最大值为
面积的最大值为![]() .
.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 为自然对数的底数) .
为自然对数的底数) .
(1)若![]() 在
在![]() 处的取得极值为1,求
处的取得极值为1,求![]() 及
及![]() 的值;
的值;
(2)![]() 时,讨论函数
时,讨论函数![]() 的极值;
的极值;
(3)当![]() 时,若直线
时,若直线![]() 与曲线
与曲线![]() 没有公共点,求
没有公共点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设离心率为3,实轴长为1的双曲线![]() (
(![]() )的左焦点为
)的左焦点为![]() ,顶点在原点的抛物线
,顶点在原点的抛物线![]() 的准线经过点
的准线经过点![]() ,且抛物线
,且抛物线![]() 的焦点在
的焦点在![]() 轴上.
轴上.
(1)求抛物线![]() 的方程;
的方程;
(2)若直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,且满足
,且满足![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在综合素质评价的某个维度的测评中,依据评分细则,学生之间相互打分,最终将所有的数据合成一个分数,满分100分,按照大于或等于80分的为优秀,小于80分的为合格,为了解学生的在该维度的测评结果,在毕业班中随机抽出一个班的数据.该班共有60名学生,得到如下的列联表:
优秀 | 合格 | 总计 | |
男生 | 6 | ||
女生 | 18 | ||
合计 | 60 |
已知在该班随机抽取1人测评结果为优秀的概率为![]() .
.
(1)完成上面的列联表;
(2)能否在犯错误的概率不超过0.10的前提下认为性别与测评结果有关系?
(3)现在如果想了解全校学生在该维度的表现情况,采取简单随机抽样方式在全校学生中抽取少数一部分来分析,请你选择一个合适的抽样方法,并解释理由.
附:
| 0.25 | 0.10 | 0.025 |
| 1.323 | 2.706 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 右焦点F的坐标为
右焦点F的坐标为![]() ,点
,点![]() 在椭圆C上,过F且斜率为
在椭圆C上,过F且斜率为![]() 的直线l与椭圆C相交于A,B两点,线段AB的中点为M,O为坐标原点.
的直线l与椭圆C相交于A,B两点,线段AB的中点为M,O为坐标原点.
(I)求椭圆C的方程;
(Ⅱ)设线段AB的垂直平分线与x轴、y轴分别相交于点C,D.若![]() 与
与![]() 的面积相等,求直线l的斜率k.
的面积相等,求直线l的斜率k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2017年第一季度五省GDP情况图,则下列陈述中不正确的是( )

A.2017年第一季度GDP增速由高到低排位第5的是浙江省
B.2017年第一季度GDP总量和增速由高到低排位均居同一位的省只有1个
C.去年同期河南省的GDP总量不超过4000亿元
D.与去年同期相比,2017年第一季度五个省的GDP总量均实现了增长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com