
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点,现将
的中点,现将![]() 与
与![]() 折起,使得平面
折起,使得平面![]() 及平面
及平面![]() 都与平面
都与平面![]() 垂直.
垂直.

(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() ,利用面面垂直的性质定理证明
,利用面面垂直的性质定理证明![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,可得出
,可得出![]() ,并证明出
,并证明出![]() ,可证明出四边形
,可证明出四边形![]() 为平行四边形,于是有
为平行四边形,于是有![]() ,再利用直线与平面平行的判定定理可证明出
,再利用直线与平面平行的判定定理可证明出![]() 平面
平面![]() ;
;
(2)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,利用空间向量法可计算出二面角
,利用空间向量法可计算出二面角![]() 的余弦值.
的余弦值.
(1)过点![]() 作
作![]() 于
于![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,连接
,连接![]() .
.
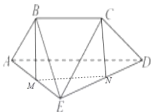
![]() 平面
平面![]() 及平面
及平面![]() 都与平面
都与平面![]() 垂直,
垂直,
平面![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,同理可证
,同理可证![]() 平面
平面![]() ,
,![]() .
.
![]() 矩形
矩形![]() 中,
中,![]() 与
与![]() 全等,
全等,![]() .
.
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
(2)矩形![]() 中,
中,![]() ,以
,以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,
,
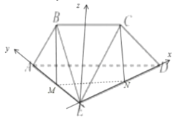
则![]() 、
、![]() 、
、![]() ,
,
![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则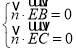 ,即
,即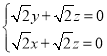 ,
,
令![]() ,得
,得![]() ,则
,则![]() ,
,
易得平面![]() 的法向量为
的法向量为![]() ,
,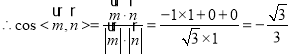 ,
,
因此,二面角![]() 的余弦值为
的余弦值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 交于点
交于点![]() ,曲线
,曲线![]() 与
与![]() 轴交于点
轴交于点![]() ,求线段
,求线段![]() 的中点到点
的中点到点![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
在平面直角坐标系中,以坐标原点O为极点,x轴正半轴为极轴,建立极坐标系,已知曲线C的极坐标方程为:![]() ,经过点
,经过点![]() ,倾斜角为
,倾斜角为![]() 的直线l与曲线C交于A,B两点
的直线l与曲线C交于A,B两点
(I)求曲线C的直角坐标方程和直线l的参数方程;
(Ⅱ)求![]() 的值。
的值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】图(![]() )是某品牌汽车
)是某品牌汽车![]() 年月销量统计图,图(
年月销量统计图,图(![]() )是该品牌汽车月销量占所属汽车公司当月总销量的份额统计图,则下列说法错误的是( )
)是该品牌汽车月销量占所属汽车公司当月总销量的份额统计图,则下列说法错误的是( )
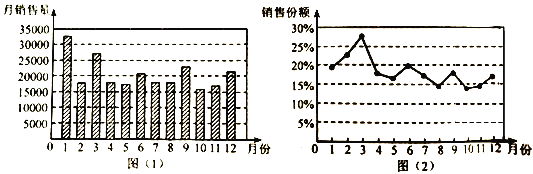
A.该品牌汽车![]() 年全年销量中,
年全年销量中,![]() 月份月销量最多
月份月销量最多
B.该品牌汽车![]() 年上半年的销售淡季是
年上半年的销售淡季是![]() 月份,下半年的销售淡季是
月份,下半年的销售淡季是![]() 月份
月份
C.![]() 年该品牌汽车所属公司
年该品牌汽车所属公司![]() 月份的汽车销量比
月份的汽车销量比![]() 月份多
月份多
D.该品牌汽车![]() 年下半年月销量相对于上半年,波动性小,变化较平稳
年下半年月销量相对于上半年,波动性小,变化较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了鼓励职员工作热情,某公司对每位职员一年来的工作业绩按月进行考评打分;年终按照职员的月平均值评选公司最佳职员并给予相应奖励.已知职员![]() 一年来的工作业绩分数的茎叶图如图所示:
一年来的工作业绩分数的茎叶图如图所示:
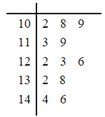
(1)根据职员![]() 的业绩茎叶图求出他这一年的工作业绩的中位数和平均数;
的业绩茎叶图求出他这一年的工作业绩的中位数和平均数;
(2)若记职员![]() 的工作业绩的月平均数为
的工作业绩的月平均数为![]() .
.
①已知该公司还有6位职员的业绩在100以上,分别是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,在这6人的业绩里随机抽取2个数据,求恰有1个数据满足
,在这6人的业绩里随机抽取2个数据,求恰有1个数据满足![]() (其中
(其中![]() )的概率;
)的概率;
②由于职员![]() 的业绩高,被公司评为年度最佳职员,在公司年会上通过抽奖形式领取奖金.公司准备了9张卡片,其中有1张卡片上标注奖金为6千元,4张卡片的奖金为4千元,另外4张的奖金为2千元.规则是:获奖职员需要从9张卡片中随机抽出3张,这3张卡片上的金额数之和就是该职员所得奖金.记职员
的业绩高,被公司评为年度最佳职员,在公司年会上通过抽奖形式领取奖金.公司准备了9张卡片,其中有1张卡片上标注奖金为6千元,4张卡片的奖金为4千元,另外4张的奖金为2千元.规则是:获奖职员需要从9张卡片中随机抽出3张,这3张卡片上的金额数之和就是该职员所得奖金.记职员![]() 获得的奖金为
获得的奖金为![]() (千元),求
(千元),求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,将曲线
,将曲线![]() 向左平移
向左平移![]() 个单位长度得到曲线
个单位长度得到曲线![]() .
.
(1)求曲线![]() 的参数方程;
的参数方程;
(2)已知![]() 为曲线
为曲线![]() 上的动点,
上的动点, ![]() 两点的极坐标分别为
两点的极坐标分别为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中![]() ,以原点
,以原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,直线
轴正半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为:
的参数方程为: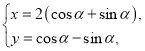 (
(![]() 为参数),
为参数),![]() ,
,![]() 为直线
为直线![]() 上距离为
上距离为![]() 的两动点,点
的两动点,点![]() 为曲线
为曲线![]() 上的动点且不在直线
上的动点且不在直线![]() 上.
上.
(1)求曲线![]() 的普通方程及直线
的普通方程及直线![]() 的直角坐标方程.
的直角坐标方程.
(2)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
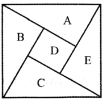
【题目】如图为我国数学家赵爽(约3世纪初)在为《周牌算经》作注时验证勾股定理的示意图,现在提供6种不同的颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则![]() ,
,![]() 区域涂同色的概率为( )
区域涂同色的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com