练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】一个四棱锥的三视图如图所示，关于这个四棱锥，下列说法正确的是（ ）

    A. 最长的棱长为

    B. 该四棱锥的体积为

    C. 侧面四个三角形都是直角三角形

    D. 侧面三角形中有且仅有一个等腰三角形

    【答案】B

    【解析】还原四棱锥，如图所示，由主视图可知，底面 计算可知B正确，故选B．

    点睛: 思考三视图还原空间几何体首先应深刻理解三视图之间的关系，遵循“长对正，高平齐，宽相等”的基本原则，其内涵为正视图的高是几何体的高，长是几何体的长；俯视图的长是几何体的长，宽是几何体的宽；侧视图的高是几何体的高，宽是几何体的宽.由三视图画出直观图的步骤和思考方法：1、首先看俯视图，根据俯视图画出几何体地面的直观图；2、观察正视图和侧视图找到几何体前、后、左、右的高度；3、画出整体，然后再根据三视图进行调整.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x2+ax+b﹣a（a，b∈R）．
    （1）若关于x的不等式f（x）＞0的解集为（﹣∞，﹣1）∪（3，+∞），求实数a，b的值；
    （2）设a=2，若不等式f（x）＞b2﹣3b对任意实数x都成立，求实数b的取值范围；
    （3）设b=3，解关于x的不等式组 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=（x2+ax﹣2a2+3a）ex（x∈R），其中a∈R．
    （1）当a=0时，求曲线y=f（x）在点（1，f（1））处的切线方程；
    （2）当 时，求函数f（x）的单调区间和极值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= 的定义域为（﹣1，1），满足f（﹣x）=﹣f（x），且f（ ）= ．
    （1）求函数f（x）的解析式；
    （2）证明f（x）在（﹣1，1）上是增函数；
    （3）解不等式f（x2﹣1）+f（x）＜0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设入射光线沿直线y=2x+1射向直线y=x，则被y=x反射后，反射光线所在的直线方程是（ ）
    A.x﹣2y﹣1=0
    B.x﹣2y+1=0
    C.3x﹣2y+1=0
    D.x+2y+3=0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，AA1B1B是圆柱的轴截面，C是底面圆周上异于A，B的一点，AA1=AB=2．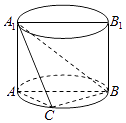
    （1）求证：平面AA1C⊥平面BA1C；
    （2）若AC=BC，求几何体A1﹣ABC的体积V．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= （x2﹣2ax+3）．
    （1）若f（x）的定义域为R，求a的取值范围；
    （2）若f（﹣1）=﹣3，求f（x）单调区间；
    （3）是否存在实数a，使f（x）在（﹣∞，2）上为增函数？若存在，求出a的范围？若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设二次函数，关于的不等式的解集有且只有一个元素．

    （1）设数列的前项和，求数列的通项公式；

    （2）记，则数列中是否存在不同的三项成等比数列？若存在，求出这三项，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线C：y2=2px（p＞0），上的点M（1，m）到其焦点F的距离为2，
    （1）求C的方程；并求其准线方程；
    （2）已知A （1，﹣2），是否存在平行于OA（O为坐标原点）的直线L，使得直线L与抛物线C有公共点，且直线OA与L的距离等于 ？若存在，求直线L的方程；若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案