
分析 (1)由定义域为R得kx2+kx+1>0恒成立,然后根据k的取值讨论即可;
(2)由值域为R得(0,+∞)⊆{y|y=kx2+kx+1},转化为二次函数问题解决.
解答 解:(1)∵y=lg(kx2+kx+1)定义域为R,
∴kx2+kx+1>0恒成立.
令g(x)=kx2+kx+1,
①当k=0时,g(x)=1符合题意;
②当k<0时,g(x)为开口向下的二次函数,显然不符合题意;
③当k>0时,g(x)为开口向上的二次函数,gmin(x)=$\frac{4k-{k}^{2}}{4k}$=1-$\frac{k}{4}$,令1-$\frac{k}{4}$>0得0<k<4.
综上所述:k的取值范围是[0,4).
(2))设g(x)=kx2+kx+1值域为A.
∵y=lg(kx2+kx+1)值域为R,
∴(0,+∞)⊆A.
∴g(x)为开口向上的二次函数,且gmin(x)≤0,
∴△=k2-4k≥0,解得k≤0,或k≥4.
∴k的取值范围是(-∞,0]∪[4,+∞).
点评 本题考查了对数函数的定义域,值域,二次不等式的解法和分类讨论思想,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
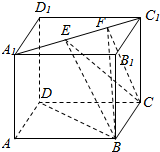 如图,棱长为1的正方体ABCD-A1B1C1D1中,E,F为A1C1上的动点,且EF=$\frac{1}{2}$,则下列结论中错误的是( )
如图,棱长为1的正方体ABCD-A1B1C1D1中,E,F为A1C1上的动点,且EF=$\frac{1}{2}$,则下列结论中错误的是( )| A. | BD⊥CE | |
| B. | △CEF的面积为定值 | |
| C. | 四面体BCEF的体积随EF的位置的变化而变化 | |
| D. | 直线BE与CF为异面直线 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{7}$ | B. | -$\sqrt{7}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<a<b | B. | c<b<a | C. | a<b<c | D. | a<c<b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①与② | B. | ①与④ | C. | ②与③ | D. | ②与④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com