
已知集合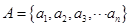 ,
,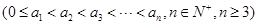
具有性质 :对任意的
:对任意的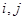
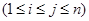 ,
,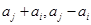 至少有一个属于
至少有一个属于 .
.
(1)分别判断集合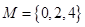 与
与 是否具有性质
是否具有性质 ;
;
(2)求证:①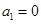 ;
;
②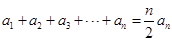 ;
;
(3)当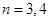 或
或 时集合
时集合 中的数列
中的数列 是否一定成等差数列?说明理由.
是否一定成等差数列?说明理由.
(1) 有 ,
有 , 没有;(2)证明见解析;(3)
没有;(2)证明见解析;(3)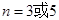 时,是等差数列,
时,是等差数列, 时,不一定.
时,不一定.
解析试题分析:(1)对于具体的集合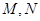 ,我们根据定义直接验证即可,如集合
,我们根据定义直接验证即可,如集合 ,
,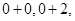
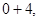
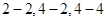 均属于集合
均属于集合 ,故
,故 个有性质
个有性质 ,而集合
,而集合 ,
,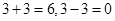 均不属于
均不属于 ,则
,则 不具有性质
不具有性质 ;(2)
;(2)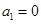 易证,等式
易证,等式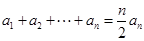 变形得
变形得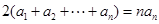 ,联想到等差数列的前
,联想到等差数列的前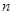 项和求法,是不是有
项和求法,是不是有 (这是成立的),
(这是成立的),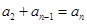 (?),
(?), (?),…,由于
(?),…,由于 ,故
,故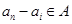 ,从而可看出只能是
,从而可看出只能是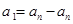 ,
,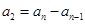 ,
,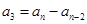 ,…,
,…,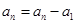 ,即
,即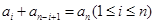 成立,②式得证;(3)如果答案是肯定的,必须证明,如果答案是不确定的,则要举例说明,
成立,②式得证;(3)如果答案是肯定的,必须证明,如果答案是不确定的,则要举例说明, 时,集合
时,集合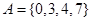 具有性质
具有性质 ,但不是等差数列,
,但不是等差数列,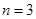 和
和 时,具有性质
时,具有性质 的集合
的集合 中的数列是等差数列,
中的数列是等差数列,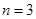 时易证,首先
时易证,首先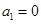 ,然后
,然后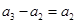 ,即
,即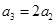 ,故
,故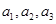 成等差,
成等差,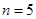 时,难一点,由(2)知
时,难一点,由(2)知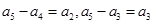 ,两式相减可得
,两式相减可得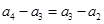 ,而由于
,而由于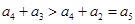 ,即
,即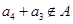 ,则有
,则有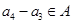 ,注意到
,注意到 ,于是
,于是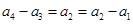 ,又有
,又有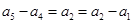 ,故数列
,故数列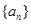 是等差数列,
是等差数列,
试题解析:(1)∵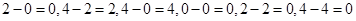 ≒∴集合
≒∴集合 具有性质
具有性质 ,
,
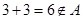 ,
,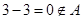 ,
, 集合
集合 不具有性质
不具有性质 . 3分
. 3分
(2)由已知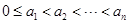 ,
,
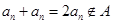 ,
,
则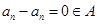 ,仍由
,仍由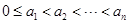 知
知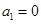 ; 5分
; 5分
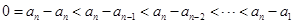

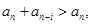


科目:高中数学 来源: 题型:解答题
(12分)(2011•湖北)成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列{bn}中的b3、b4、b5.
(Ⅰ)求数列{bn}的通项公式;
(Ⅱ)数列{bn}的前n项和为Sn,求证:数列{Sn+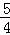 }是等比数列.
}是等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2013•浙江)在公差为d的等差数列{an}中,已知a1=10,且a1,2a2+2,5a3成等比数列.
(1)求d,an;
(2)若d<0,求|a1|+|a2|+|a3|+…+|an|.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
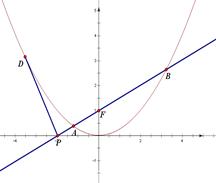
抛物线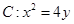 ,直线
,直线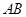 过抛物线
过抛物线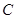 的焦点
的焦点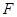 ,交
,交 轴于点
轴于点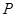 .
.
(1)求证: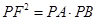 ;
;
(2)过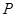 作抛物线
作抛物线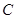 的切线,切点为
的切线,切点为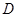 (异于原点),
(异于原点),
(ⅰ)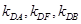 是否恒成等差数列,请说明理由;
是否恒成等差数列,请说明理由;
(ⅱ)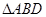 重心的轨迹是什么图形,请说明理由.
重心的轨迹是什么图形,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
下列命题正确的是 ( )
①若数列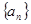 是等差数列,且
是等差数列,且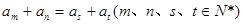 ,
,
则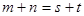 ;
;
②若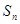 是等差数列
是等差数列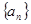 的前
的前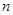 项的和,则
项的和,则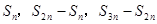 成等差数列;
成等差数列;
③若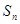 是等比数列
是等比数列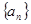 的前
的前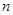 项的和,则
项的和,则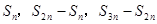 成等比数列;
成等比数列;
④若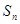 是等比数列
是等比数列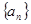 的前
的前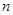 项的和,且
项的和,且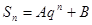 ;(其中
;(其中 是非零常数,
是非零常数,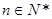 ),则
),则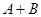 为零.
为零.
| A.①② | B.②③ | C.②④ | D.③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com