
【题目】已知函数![]()
(1)讨论![]() 的极值点的个数;
的极值点的个数;
(2)若![]() 有两个极值点x1,x2(x1<x2),且
有两个极值点x1,x2(x1<x2),且![]() 求
求![]() 的最小值
的最小值
【答案】(1)见解析;(2)![]()
【解析】
(1)求导数得![]() ,当
,当![]() 通过讨论判别式
通过讨论判别式![]() 与0的关系,得函数单调性,由单调性即可得函数的极值问题;(2)
与0的关系,得函数单调性,由单调性即可得函数的极值问题;(2)![]() 有两个极值点
有两个极值点![]() 可知
可知![]() 为方程
为方程![]() 的两个根,用
的两个根,用![]() 表示出为
表示出为![]() ,令
,令![]() ,构造函数
,构造函数![]() 求导判单调性即可得到最值.
求导判单调性即可得到最值.
(1)法一:由题意得![]() ,
,
令![]() ,即
,即![]() 。.
。.
①当![]() ,即
,即![]() 时,
时,![]() 对任意
对任意![]() 恒成立,即
恒成立,即![]() 对任意
对任意![]() 恒成立,此时
恒成立,此时![]() 没有极值点。
没有极值点。
②当![]() ,即
,即![]() 或
或![]() 时。
时。
若![]() ,设方程
,设方程![]() 的两个不同实根为
的两个不同实根为![]() ,不妨设
,不妨设![]() ,
,
则![]() ,
,
故![]() ,
,
![]() 当
当![]() 或
或![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
故![]() 是函数
是函数![]() 的两个极值点。
的两个极值点。
若![]() ,设方程
,设方程![]() 的两个不同实根为
的两个不同实根为![]() ,
,
则![]() ,故
,故![]() 。
。
![]() 当
当![]() 时,
时,![]() ,故函数
,故函数![]() 没有极值点。
没有极值点。
当![]() 时,函数
时,函数![]() 没有极值点。
没有极值点。
法二:![]() ,
,
![]() 。.
。.
①当![]() ,即
,即![]() 时,
时,![]() 对任意
对任意![]() 恒成立,
恒成立,![]() 在
在![]() 上单调递增,
上单调递增,![]() 没有极值点。.
没有极值点。.
②当![]() ,即
,即![]() 时,
时,![]() 有两个不等正实数解,设为
有两个不等正实数解,设为![]() ,
,
![]() 。
。
不妨设![]() ,则当
,则当![]() 时,
时,![]() ,
,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,
,![]() 单调递减,当
单调递减,当![]() 时,
时,![]() ,
,![]() 单调递增,所以
单调递增,所以![]() 分别为
分别为![]() 的极大值点和极小值点。
的极大值点和极小值点。
故![]() 有两个极值点。.
有两个极值点。.
综上所述,当![]() 时,
时,![]() 没有极值点,
没有极值点,
当![]() 时,
时,![]() 有两个极值点。
有两个极值点。
(2)由题意知,![]() ,
,
则易知![]() 为方程
为方程![]() 的两个根,且
的两个根,且![]() ,
,
所以![]()
![]()
![]()
![]()
![]()
![]()
记![]() ,由
,由![]() 且
且![]() 知
知![]() ,
,
则![]() ,
,
记![]() ,
,
则![]() ,
,
故![]() 在
在![]() 上单调递减。
上单调递减。
由![]() 知
知![]() ,
,
从而![]() ,即
,即![]() ,
,
故![]() ,结合
,结合![]() ,解得
,解得![]() ,
,
从而![]() 的最小值为
的最小值为![]() ,
,
即![]() 的最小值为
的最小值为![]() 。
。


科目:高中数学 来源: 题型:
【题目】为了调查一款电视机的使用时间,研究人员对该款电视机进行了相应的测试,将得到的数据统计如下图所示:

并对不同年龄层的市民对这款电视机的购买意愿作出调查,得到的数据如下表所示:
愿意购买这款电视机 | 不愿意购买这款电视机 | 总计 | |
40岁以上 | 800 | 1000 | |
40岁以下 | 600 | ||
总计 | 1200 |
(1)根据图中的数据,试估计该款电视机的平均使用时间;
(2)根据表中数据,判断是否有99.9%的把握认为“愿意购买该款电视机”与“市民的年龄”有关;
(3)若按照电视机的使用时间进行分层抽样,从使用时间在![]() 和
和![]() 的电视机中抽取5台,再从这5台中随机抽取2台进行配件检测,求被抽取的2台电视机的使用时间都在
的电视机中抽取5台,再从这5台中随机抽取2台进行配件检测,求被抽取的2台电视机的使用时间都在![]() 内的概率.
内的概率.
附: | 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】独立性检验中,假设![]() :运动员受伤与不做热身运动没有关系.在上述假设成立的情况下,计算得
:运动员受伤与不做热身运动没有关系.在上述假设成立的情况下,计算得![]() 的观测值
的观测值![]() .下列结论正确的是( )
.下列结论正确的是( )
附:
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
A. 在犯错误的概率不超过0.01的前提下,认为运动员受伤与不做热身运动有关
B. 在犯错误的概率不超过0.01的前提下,认为运动员受伤与不做热身运动无关
C. 在犯错误的概率不超过0.005的前提下,认为运动员受伤与不做热身运动有关
D. 在犯错误的概率不超过0.005的前提下,认为运动员受伤与不做热身运动无关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】流行性感冒(简称流感)是流感病毒引起的急性呼吸道感染,是一种传染性强、传播速度快的疾病.其主要通过空气中的飞沫、人与人之间的接触或与被污染物品的接触传播.流感每年在世界各地均有传播,在我国北方通常呈冬春季流行,南方有冬春季和夏季两个流行高峰.儿童相对免疫力低,在幼儿园、学校等人员密集的地方更容易被传染.某幼儿园将去年春期该园患流感小朋友按照年龄与人数统计,得到如下数据:
年龄( |
|
|
|
|
|
患病人数( |
|
|
|
|
|
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)计算变量![]() 、
、![]() 的相关系数
的相关系数![]() (计算结果精确到
(计算结果精确到![]() ),并回答是否可以认为该幼儿园去年春期患流感人数与年龄负相关很强?(若
),并回答是否可以认为该幼儿园去年春期患流感人数与年龄负相关很强?(若![]() ,则
,则![]() 、
、![]() 相关性很强;若
相关性很强;若![]() ,则
,则![]() 、
、![]() 相关性一般;若
相关性一般;若![]() ,则
,则![]() 、
、![]() 相关性较弱.)
相关性较弱.)
参考数据:![]() .
.
参考公式: ,
,
相关系数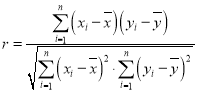 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,短轴长为
,短轴长为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 是椭圆
是椭圆![]() 的上焦点.问:是否存在直线
的上焦点.问:是否存在直线![]() ,使得
,使得![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设A,B,C,D为平面内的四点,且A(1,3),B(2,–2),C(4,1).
(1)若![]() ,求D点的坐标;
,求D点的坐标;
(2)设向量![]() ,
,![]() ,若k
,若k![]() –
–![]() 与
与![]() +3
+3![]() 平行,求实数
平行,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如图所示.假设现在青蛙在A叶上,则跳四次之后停在A叶上的概率是_________
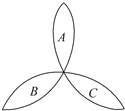
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列![]() 满足:存在正整数T,对于任意正整数n都有
满足:存在正整数T,对于任意正整数n都有![]() 成立,则称数列
成立,则称数列![]() 为周期数列,周期为T.已知数列
为周期数列,周期为T.已知数列![]() 满足
满足![]() ,
, ,则下列结论中错误的是( )
,则下列结论中错误的是( )
A.若![]() ,则m可以取3个不同的值;
,则m可以取3个不同的值;
B.若![]() ,则数列
,则数列![]() 是周期为3的数列;
是周期为3的数列;
C.对于任意的![]() 且T≥2,存在
且T≥2,存在![]() ,使得
,使得![]() 是周期为
是周期为![]() 的数列
的数列
D.存在![]() 且
且![]() ,使得数列
,使得数列![]() 是周期数列
是周期数列
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com