
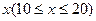 万件的该种产品所需要的总成本为
万件的该种产品所需要的总成本为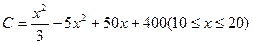 万元,市场销售情况可能出现好、中、差三种情况,各种情况发生的概率和相应的价格p(元)与年产量x之间的函数关系如下表所示.
万元,市场销售情况可能出现好、中、差三种情况,各种情况发生的概率和相应的价格p(元)与年产量x之间的函数关系如下表所示.| 市场情况 | 概率 | 价格p与产量x的函数关系式 |
| 好 | 0.3 | 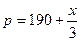 |
| 中 | 0.5 | 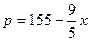 |
| 差 | 0.2 | 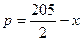 |
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源:不详 题型:解答题
 生中随机抽取50名学生测量其身高,据测量被测学生的身高全部在155cm到195cm之间.将测量结果按如下方式分成8组:第一组[155,160),第二组[160,165),……,第八组[190,195],如下图是按上述分组得到的频率分布直方图的一部分.已知:第1组与第8组的人数相同,第6组、第7组和第8组的人数依次成等差数列.
生中随机抽取50名学生测量其身高,据测量被测学生的身高全部在155cm到195cm之间.将测量结果按如下方式分成8组:第一组[155,160),第二组[160,165),……,第八组[190,195],如下图是按上述分组得到的频率分布直方图的一部分.已知:第1组与第8组的人数相同,第6组、第7组和第8组的人数依次成等差数列.| 分组 | 频数 | 频率 | 频率/组距 |
| … | … | … | … |
| [180,185) | 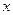 |  | z |
| [185,190) | m | n | p |
| … | … | … | … |

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 表示方案
表示方案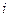 实施两年后柑桔产量达到灾前产量的倍数。
实施两年后柑桔产量达到灾前产量的倍数。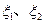 的分布列;
的分布列;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
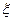 ,求
,求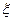 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
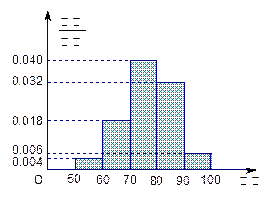
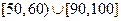 内的
内的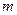 、
、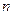 ,求事件“
,求事件“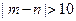 ”的概率
”的概率查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 18
18| 英语成绩 | 75~90 | 90~105 | 105~120 | 120~135 | 135~150 |
| 考生人数 | 20 | 30 | 80 | 40 | 30 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
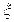 .
.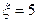 的概率
的概率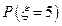 ;
;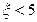 的概率
的概率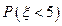 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.如果一事件发生的概率为十万分之一,说明此事件不可能发生 |
| B.如果一事件不是不可能事件,说明此事件是必然事件 |
| C.概率的大小与不确定事件有关 |
| D.如果一事件发生的概率为99.999%,说明此事件必然发生 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 次,甲射中的概率为
次,甲射中的概率为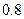 ,乙射中的概率为
,乙射中的概率为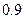 ,求:
,求: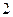 人都射中目标的概率;
人都射中目标的概率;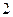 人中恰有
人中恰有 人射中目标的概率;
人射中目标的概率;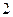 人至少有
人至少有 人射中目标的概率;
人射中目标的概率;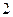 人至多有
人至多有 人射中目标的概率?
人射中目标的概率?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com