
【题目】已知函数f(x)=|x+1|.
(Ⅰ) 解不等式f(x+8)≥10﹣f(x);
(Ⅱ) 若|x|>1,|y|<1,求证:f(y)<|x|f( ![]() ).
).
【答案】(Ⅰ)解:原不等式即为|x+9|≥10﹣|x+1|. 当x<﹣9时,则﹣x﹣9≥10+x+1,解得x≤﹣10;
当﹣9≤x≤﹣1时,则x+9≥10+x+1,此时不成立;
当x>﹣1时,则x+9≥10﹣x﹣1,解得x≥0.
所以原不等式的解集为{x|x≤﹣10或x≥0}.
(Ⅱ)证明:要证 ![]() ,即
,即 ![]() ,只需证明
,只需证明 ![]() .
.
则有 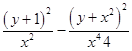 =
= 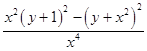 =
= ![]()
= ![]() =
= ![]() .
.
因为|x|2>1,|y|2<1,则 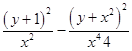 =
= ![]() ,
,
所以 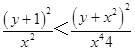 ,原不等式得证
,原不等式得证
【解析】(Ⅰ) 分类讨论,解不等式f(x+8)≥10﹣f(x);(Ⅱ)利用分析法证明不等式.
【考点精析】解答此题的关键在于理解绝对值不等式的解法的相关知识,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣a(x﹣1),g(x)=ex .
(1)求函数f(x)的单调区间;
(2)当a≠0时,过原点分别作曲线y=f(x)与y=g(x)的切线l1 , l2 , 已知两切线的斜率互为倒数,证明: ![]() <a<
<a< ![]() ;
;
(3)设h(x)=f(x+1)+g(x),当x≥0,h(x)≥1时,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险公司有一款保险产品的历史收益率(收益率=利润÷保费收入)的频率分布直方图如图所示:
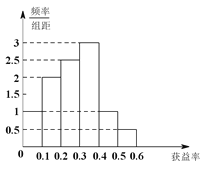
(Ⅰ)试估计平均收益率;
(Ⅱ)根据经验,若每份保单的保费在20元的基础上每增加![]() 元,对应的销量
元,对应的销量![]() (万份)与
(万份)与![]() (元)有较强线性相关关系,从历史销售记录中抽样得到如下5组
(元)有较强线性相关关系,从历史销售记录中抽样得到如下5组![]() 与
与![]() 的对应数据:
的对应数据:

据此计算出的回归方程为![]() .
.
(i)求参数![]() 的估计值;
的估计值;
(ii)若把回归方程![]() 当作
当作![]() 与
与![]() 的线性关系,用(Ⅰ)中求出的平均收益率估计此产品的收益率,每份保单的保费定为多少元时此产品可获得最大收益,并求出该最大收益.
的线性关系,用(Ⅰ)中求出的平均收益率估计此产品的收益率,每份保单的保费定为多少元时此产品可获得最大收益,并求出该最大收益.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某旅游爱好者计划从3个亚洲国家 ![]() 和3个欧洲国家
和3个欧洲国家 ![]() 中选择2个国家去旅游.
中选择2个国家去旅游.
(Ⅰ)若从这6个国家中任选2个,求这2个国家都是亚洲国家的概率;
(Ⅱ)若从亚洲国家和欧洲国家中各任选1个,求这2个国家包括 ![]() 但不包括
但不包括 ![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】潮州统计局就某地居民的月收入调查了![]() 人,并根据所得数据画了样本的频率分
人,并根据所得数据画了样本的频率分
布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在![]() )。
)。

(1)求居民月收入在![]() 的频率;
的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这![]() 人中分层抽样方法抽出
人中分层抽样方法抽出![]() 人作进一步分析,则月收入在
人作进一步分析,则月收入在![]() 的这段应抽多少人?
的这段应抽多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学从高三男生中随机抽取100名学生,将他们的身高数据进行整理,得到下侧的频率分布表.
组号 | 分组 | 频率 |
第1组 | [160,165) | 0.05 |
第2组 |
| 0.35 |
第3组 |
| 0.3 |
第4组 |
| 0.2 |
第5组 |
| 0.1 |
合计 | 1.00 | |
(Ⅰ)为了能对学生的体能做进一步了解,该校决定在第3,4,5组中用分层抽样的方法抽取6名学生进行体能测试,问第3,4,5组每组各应抽取多少名学生进行测试;
(Ⅱ)在(Ⅰ)的前提下,学校决定在6名学生中随机抽取2名学生进行引体向上测试,求第3组中至少有一名学生被抽中的概率;
(Ⅲ)试估计该中学高三年级男生身高的中位数位于第几组中,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以点![]() 为圆心的圆过点
为圆心的圆过点![]() 和
和![]() ,线段
,线段![]() 的垂直平分线交圆
的垂直平分线交圆![]() 于点
于点![]() 、
、![]() ,且
,且![]() ,
,
(1)求直线![]() 的方程; (2)求圆
的方程; (2)求圆![]() 的方程。
的方程。
(3)设点![]() 在圆
在圆![]() 上,试探究使
上,试探究使![]() 的面积为 8 的点
的面积为 8 的点![]() 共有几个?证明你的结论
共有几个?证明你的结论
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com