(Ⅰ)解:由题意知:a
2=4,b
2=3,∴c
2=a
2-b
2=1,得到c=1.
∴焦点坐标为(±1,0);
离心率
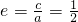
.
(Ⅱ)证明:由题意知:直线PB的斜率存在,设直线PB的方程为y=k(x-4)
设B(x
1,y
1),E(x
2,y
2),则A(x
1,-y
1).
由

得(3+4k
2)x
2-32k
2x+64k
2-12=0
则
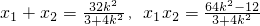
…(1)
直线AE的方程为
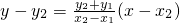
,
令y=0,得
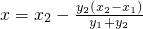
…(2)
又y
1=k(x
1-4),y
2=k(x
2-4)代入(2)式,得
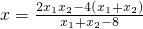
…(3)
把(1)代入(3)式,整理得x=1
所以直线AE与x轴相交于定点(1,0).
分析:(I)由椭圆的标准方程得到:a
2=4,b
2=3,c
2=a
2-b
2,即可得到焦点坐标和离心率;
(II)由题意知:直线PB的斜率存在,设直线PB的方程为y=k(x-4),设B(x
1,y
1),E(x
2,y
2),则A(x
1,-y
1).把直线PB的方程与椭圆的方程联立得到根与系数的关系,写出直线AE的方程,并令y
A=0,即可得到点A的横坐标的表达式,把根与系数的关系式代入即可证明.
点评:熟练掌握椭圆的标准方程及其性质、直线与椭圆相交问题转化为直线PB的方程与椭圆的方程联立得到根与系数的关系是解题的关键.

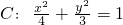 和点P(4,0),垂直于x轴的直线与椭圆C交于A,B两点,连结PB交椭圆C于另一点E.
和点P(4,0),垂直于x轴的直线与椭圆C交于A,B两点,连结PB交椭圆C于另一点E.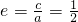 .
. 得(3+4k2)x2-32k2x+64k2-12=0
得(3+4k2)x2-32k2x+64k2-12=0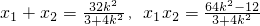 …(1)
…(1)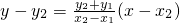 ,
,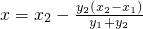 …(2)
…(2)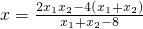 …(3)
…(3)

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案