
【题目】如图,已知AD是△ABC内角∠BAC的角平分线. 
(1)用正弦定理证明: ![]() ;
;
(2)若∠BAC=120°,AB=2,AC=1,求AD的长.
【答案】
(1)解:∵AD是∠BAC的角平分线,∴∠BAD=∠CAD,
根据正弦定理,在△ABD中, ![]() =
= ![]() ,
,
在△ADC中, ![]() =
= ![]() ,
,
∵sin∠ADB=sin(π﹣∠ADC)=sin∠ADC,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴ ![]()
(2)解:根据余弦定理,cos∠BAC= ![]() ,
,
即cos120°= ![]() ,
,
解得BC= ![]() ,
,
又 ![]() ,
,
∴ ![]() =
= ![]() ,
,
解得CD= ![]() ,BD=
,BD= ![]() ;
;
设AD=x,则在△ABD与△ADC中,
根据余弦定理得,
cos60°= 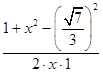 ,
,
且cos60°= 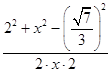 ,
,
解得x= ![]() ,即AD的长为
,即AD的长为 ![]()
【解析】(1)根据AD是∠BAC的角平分线,利用正弦定理,即可证明结论成立;(2)根据余弦定理,先求出BC的值,再利用角平分线和余弦定理,即可求出AD的长.
【考点精析】掌握正弦定理的定义和余弦定理的定义是解答本题的根本,需要知道正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() .
.


科目:高中数学 来源: 题型:
【题目】几年来,网上购物风靡,快递业迅猛发展,某市的快递业务主要由两家快递公司承接,即圆通公司与申通公司:“快递员”的工资是“底薪+送件提成”:这两家公司对“快递员”的日工资方案为:圆通公司规定快递员每天底薪为70元,每送件一次提成1元;申通公司规定快递员每天底薪为120元,每日前83件没有提成,超过83件部分每件提成10元,假设同一公司的快递员每天送件数相同,现从这两家公司各随机抽取一名快递员并记录其100天的送件数,得到如下条形图: 
(1)求申通公司的快递员一日工资y(单位:元)与送件数n的函数关系;
(2)若将频率视为概率,回答下列问题: ①记圆通公司的“快递员”日工资为X(单位:元),求X的分布列和数学期望;
②小王想到这两家公司中的一家应聘“快递员”的工作,如果仅从日收入的角度考虑,请你利用所学过的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)= ![]() sinxcosx+sin2x的图象上各点的纵坐标不变,横坐标变为原来的2倍,再沿x轴向右平移
sinxcosx+sin2x的图象上各点的纵坐标不变,横坐标变为原来的2倍,再沿x轴向右平移 ![]() 个单位,得到函数y=g(x)的图象,则y=g(x)的一个递增区间是( )
个单位,得到函数y=g(x)的图象,则y=g(x)的一个递增区间是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为D,若对于a,b,c∈D,f(a),f(b),f(c)分别为某个三角形的边长,则称f(x)为“三角形函数”.给出下列四个函数: ①f(x)=lnx(e2≤x≤e3);②f(x)=4﹣cosx;③ ![]() ;④
;④ ![]() .
.
其中为“三角形函数”的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+alnx﹣x(a≠0),g(x)=x2 . (Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若对于任意的a∈(1,+∞),总存在x1 , x2∈[1,a],使得f(x1)﹣f(x2)>g(x1)﹣g(x2)+m成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=e2x﹣ax2+bx﹣1,其中a,b∈R,e为自然对数的底数,若f(1)=0,f′(x)是f(x)的导函数,函数f′(x)在区间(0,1)内有两个零点,则a的取值范围是( )
A.(e2﹣3,e2+1)
B.(e2﹣3,+∞)
C.(﹣∞,2e2+2)
D.(2e2﹣6,2e2+2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足Sn=2an﹣2,若数列{bn}满足bn=10﹣log2an , 则使数列{bn}的前n项和取最大值时的n的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com