
【题目】若点( ![]() ,2)在幂函数f(x)的图象上,点(2,
,2)在幂函数f(x)的图象上,点(2, ![]() )在幂函数g(x)的图象上,定义h(x)=
)在幂函数g(x)的图象上,定义h(x)= ![]() 求函数h(x)的最大值及单调区间.
求函数h(x)的最大值及单调区间.
【答案】解:设f(x)=xn , g(x)=xm , 由题意可得2=( ![]() )n , 解得n=2,
)n , 解得n=2,
即有f(x)=x2;![]() =2m , 解得m=﹣1,即有g(x)=x﹣1 .
=2m , 解得m=﹣1,即有g(x)=x﹣1 .
由f(x)=g(x),可得x=1,
即有h(x)=  ;
;
当0<x≤1时,h(x)递增,可得0<h(x)≤1;
当x>1或x<0时,h(x)递减,可得h(x)∈(0,1)∪(﹣∞,0),
即有h(x)的最大值为1;
增区间为(0,1];减区间为(﹣∞,0),(1,+∞)
【解析】设f(x)=xn , g(x)=xm , 代入点的坐标,解方程可得f(x),g(x)的解析式,再由定义,求得h(x)的解析式,通过二次函数和反比例函数的性质,可得最大值和单调区间.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点. 
(1)求证:平面PAB∥平面EFG;
(2)在线段PB上确定一点Q,使PC⊥平面ADQ,并给出证明;
(3)求出D到平面EFG的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有一个关于平面图形的命题:如图,同一个平面内有两个边长都是a的正方形,其中一个的某顶点在另一个的中心,则这两个正方形重叠部分的面积恒为 ![]() .类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 .
.类比到空间,有两个棱长均为a的正方体,其中一个的某顶点在另一个的中心,则这两个正方体重叠部分的体积恒为 . 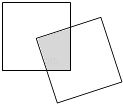
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
某学校简单随机抽样方法抽取了100名同学,对其日均课外阅读时间:(单位:分钟)进行调查,结果如下:

若将日均课外阅读时间不低于60分钟的学生称为“读书迷”
(1)将频率视为概率,估计该校4000名学生中“读书迷”有多少人?
(2)从已抽取的8名“读书迷”中随机抽取4位同学参加读书日宣传活动.
①求抽取的4为同学中有男同学又有女同学的概率;
②记抽取的“读书迷”中男生人数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=2+log3x,x∈[1,9],g(x)=[f(x)]2+f(x2),
(1)求g(x)的定义域;
(2)求g(x)的最大值以及g(x)取最大值时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg)其频率分布直方图如下:
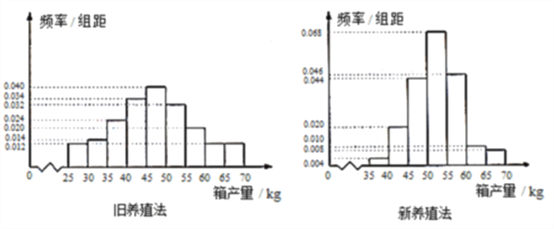
(1) 记![]() 表示事件“旧养殖法的箱产量低于50kg”,估计
表示事件“旧养殖法的箱产量低于50kg”,估计![]() 的概率;
的概率;
(2)填写下面联表,并根据列联表判断是否有![]() %的把握认为箱产量与养殖方法有关:
%的把握认为箱产量与养殖方法有关:
箱产量 | 箱产量 | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,对两种养殖方法的优劣进行比较.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
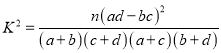
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数f(x)= ![]() 是奇函数.
是奇函数.
(Ⅰ)求a,b的值;
(Ⅱ)若对任意的t∈R,不等式f(t2﹣2t)+f(2t2﹣k)<0恒成立,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() )x , g(x)=x2 , 对于不相等的实数x1 , x2 , 设m=
)x , g(x)=x2 , 对于不相等的实数x1 , x2 , 设m= ![]() ,n=
,n= ![]() ,则下列说法正确的有( )
,则下列说法正确的有( )
①对于任意不相等的实数x1 , x2 , 都有m<0;
②对于任意不相等的实数x1 , x2 , 都有n<0;
③存在不相等的实数x1 , x2 , 使得m=n.
A.①
B.①③
C.②③
D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com