
【题目】设椭圆 ![]() 的离心率
的离心率 ![]() ,椭圆上一点A到椭圆C两焦点的距离之和为4.
,椭圆上一点A到椭圆C两焦点的距离之和为4.
(1)求椭圆C的方程;
(2)直线l与椭圆交于A,B两点,且AB中点为 ![]() ,求直线l方程.
,求直线l方程.
【答案】
(1)解:由点A到椭圆C两焦点的距离之和为4,
由椭圆的定义可得2a=4,即a=2,
又e= ![]() =
= ![]() ,可得c=
,可得c= ![]() ,
,
b= ![]() =
= ![]() ,
,
即有椭圆C的方程为 ![]() =1
=1
(2)解:中点M代入椭圆方程,可得 ![]() +
+ ![]() <1,
<1,
即M在椭圆内,
设A(x1,y1),B(x2,y2),
可得x12+2y12=4,x22+2y22=4,
两式相减可得(x1﹣x2)(x1+x2)+2(y1﹣y2)(y1+y2)=0,
由中点坐标公式可得x1+x2=﹣2,y1+y2=1,
可得直线AB的斜率为k= ![]() =﹣
=﹣ ![]() =﹣
=﹣ ![]() =1,
=1,
即有直线l的方程为y﹣ ![]() =x+1,
=x+1,
即为2x﹣2y+3=0.
【解析】(1)由椭圆的定义可得2a=4,即a=2,再由离心率公式和a,b,c的关系,求得b,进而得到椭圆方程;(2)判断中点M在椭圆内,设A(x1 , y1),B(x2 , y2),代入椭圆方程,运用作差法和中点坐标公式及斜率公式可得直线l的斜率,再由点斜式方程可得直线的方程.


科目:高中数学 来源: 题型:
【题目】某村投资128万元建起了一处生态采摘园,预计在经营过程中,第一年支出10万元,以后每年支出都比上一年增加4万元,从第一年起每年的销售收入都为76万元.设y表示前n(n∈N*)年的纯利润总和(利润总和=经营总收入﹣经营总支出﹣投资).
(1)该生态园从第几年开始盈利?
(2)该生态园前几年的年平均利润最大,最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产一种机器的固定成本为0.5万元,但每生产1百台时,又需可变成本(即另增加投入)0.25万元.市场对此商品的年需求量为5百台,销售的收入(单位:万元)函数为:R(x)=5x﹣ ![]() x2(0≤x≤5),其中x是产品生产的数量(单位:百台).
x2(0≤x≤5),其中x是产品生产的数量(单位:百台).
(1)将利润表示为产量的函数;
(2)年产量是多少时,企业所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆x2+y2+x﹣6y+m=0和直线x+2y﹣3=0交于P、Q两点,
(1)求实数m的取值范围;
(2)求以PQ为直径且过坐标原点的圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0且a≠1,设
命题p:函数y=logax在区间(0,+∞)内单调递减;
q:曲线y=x2+(2a﹣3)x+1与x轴有两个不同的交点,
如果p∧q为真命题,试求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD中边长为1,P、Q分别为BC、CD上的点,△CPQ周长为2. 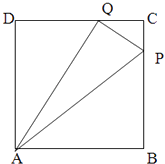
(1)求PQ的最小值;
(2)试探究求∠PAQ是否为定值,若是给出证明;不是说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某工厂对一批新产品长度(单位:mm)检测结果的频率分布直方图.估计这批产品的中位数为( ) 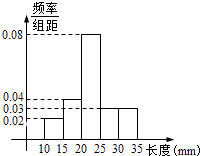
A.20
B.25
C.22.5
D.22.75
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com