
【题目】如图,E,F分别为边长为2的正方形ABCD的边BC,CD的中点,沿图中虚线折起,使得B,C,D三点重合于点O,点O在平面AEF上的射影H.
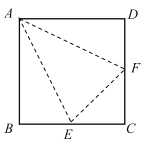
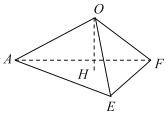
(1)求证:面![]() 面OEA;
面OEA;
(2)求证:点H是![]() 的垂心;
的垂心;
(3)求OH的长.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面几何中,与三角形的三条边所在直线的距离相等的点有且只有四个.类似的:在立体几何中,与正四面体的六条棱所在直线的距离相等的点 ( )
A. 有且只有一个 B. 有且只有三个 C. 有且只有四个 D. 有且只有五个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型企业为鼓励员工利用网络进行营销,准备为员工办理手机流量套餐.为了解员工手机流量使用情况,通过抽样,得到100位员工每人手机月平均使用流量L(单位:M)的数据,其频率分布直方图如图.
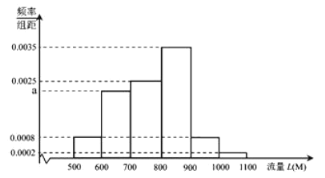
(1)从该企业的100位员工中随机抽取1人,求手机月平均使用流量不超过900M的概率;
(2)据了解,某网络运营商推出两款流量套餐,详情如下:
套餐名称 | 月套餐费(单位:元) | 月套餐流量(单位:M) |
A | 20 | 700 |
B | 30 | 1000 |
流量套餐的规则是:每月1日收取套餐费.如果手机实际使用流量超出套餐流量,则需要购买流量叠加包,每一个叠加包(包含200M的流量)需要10元,可以多次购买,如果当月流量有剩余,将会被清零.该企业准备订购其中一款流量套餐,每月为员工支付套餐费,以及购买流量叠加包所需月费用.若以平均费用为决策依据,该企业订购哪一款套餐更经济?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:2x-y+2=0与l2:x+2y-4=0,点P(1, m).
(Ⅰ)若点P到直线l1, l2的距离相等,求实数m的值;
(Ⅱ)当m=1时,已知直线l经过点P且分别与l1, l2相交于A, B两点,若P恰好
平分线段AB,求A, B两点的坐标及直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线C:![]() ,O为坐标原点,F为C的右焦点,过F的直线与C的两条渐近线的交点分别为M、N.若
,O为坐标原点,F为C的右焦点,过F的直线与C的两条渐近线的交点分别为M、N.若![]() OMN为直角三角形,则|MN|=
OMN为直角三角形,则|MN|=
A. ![]() B. 3 C.
B. 3 C. ![]() D. 4
D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校为了奖励评选出来的15名“校园科技小小发明家”,设置了一、二、三等奖:
①一等奖1000元/名,二等奖600元/名,三等奖400元/名,奖金总额不超过9000元;
②一等奖人数不得超过二等奖人数,二等奖人数不得超过三等奖人数.
则三等奖的奖金总额最少为( )
A.2400元B.3000元C.6000元D.6600元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com