Question

设变量x，y满足|x|+|y|≤2，则2x+y的最大值与最小值之和为________．

Answer 1

0
分析：作出题中不等式组表示的平面区域，得如图的四边形ABCD其内部．再将目标函数z=2x+y对应的直线进行平移，可得当x=2，y=0时，z取得最大值；当x=-2，y=0时，z取得最小值，由此即可得到本题答案．
解答：将不等式去绝对值，化简整理，则|x|+|y|≤2可化为：


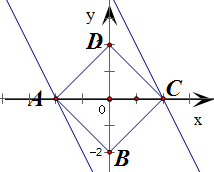
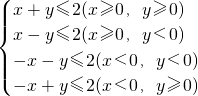
作出不等式组表示的平面区域，得如右图所示的四边形ABCD，
其中A（-2，0），B（0，2），C（2，0），D（0，-2）
将直线z=2x+y进行平移，可知当直线经过A点时z达到最小值，
当直线经过B点时z达到最小值，
∴当x=2，y=0时2x+y取最大值4；当x=-2，y=0时2x+y取最小值-4
因此，2x+y的最大值与最小值之和为0
故答案为：0
点评：本题给出二元一次不等式组，求目标函数z=2x+y的最大值和最小值之和，着重考查了二元一次不等式组表示的平面区域和简单的线性规划等知识，属于基础题．